5. Стереометрия
 Читать 0 мин.
Читать 0 мин.
5.4. Сечения
Сечения
Сечение – планиметрическая фигура, образованная рассечением объемного тела. Сечение должно образовывать единую фигуру (быть замкнутым). Построение сечения делается по строгим правилам и принципам, которые, в свою очередь, основываются на аксиомы и теоремы стереометрии.
СЕЧЕНИЯ МНОГОГРАННИКОВ
Сечение многогранника плоскостью - плоский многоугольник, у которого:
- вершины принадлежат ребрам,
- а стороны – граням многогранника.
Две соседние вершины сечения принадлежат одной грани многогранника.
ПРИНЦИПЫ ПОСТРОЕНИЯ СЕЧЕНИЙ МНОГОГРАННИКОВ:
1. Если две точки сечения принадлежат одной грани, то эти точки можно соединить.

Пример:
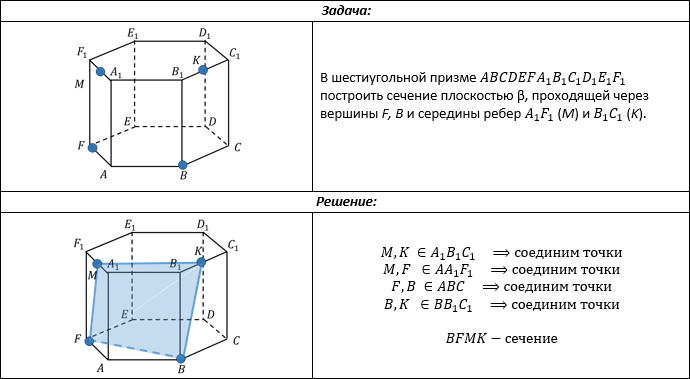

2. Если известна линия, по которой плоскость пересекает одну из параллельных граней, то вторую грань плоскость пересечет по линии, параллельной данной.

Большое значение для этого принципа имеет именно третье свойство – свойство параллельных плоскостей.
Пример:

МЕТОД СЛЕДОВ
Особенным методом построения сечений в многогранниках является метод следов. Для начала, разберемся, что такое «след».
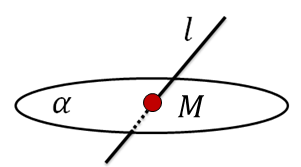
|
|
След –точка M |
|
След плоскости на плоскости – прямая, по которой плоскость пересекает плоскость . |
След прямой l на плоскости – точка пересечения прямой l с плоскостью . |
Суть метода: уже известные стороны сечения на гранях многогранника мы продолжаем за пределы стереометрической фигуры до пересечения с ребрами многогранника. Благодаря этому мы получаем «следы» этих прямых на гранях многогранника, то есть точки. Получив две точки на одной грани, мы, воспользовавшись первым принципом, можем их соединить.
Пример:

СЕЧЕНИЯ ТЕЛ ВРАЩЕНИЯ:
ЦИЛИНДР
Характерные сечения цилиндра:
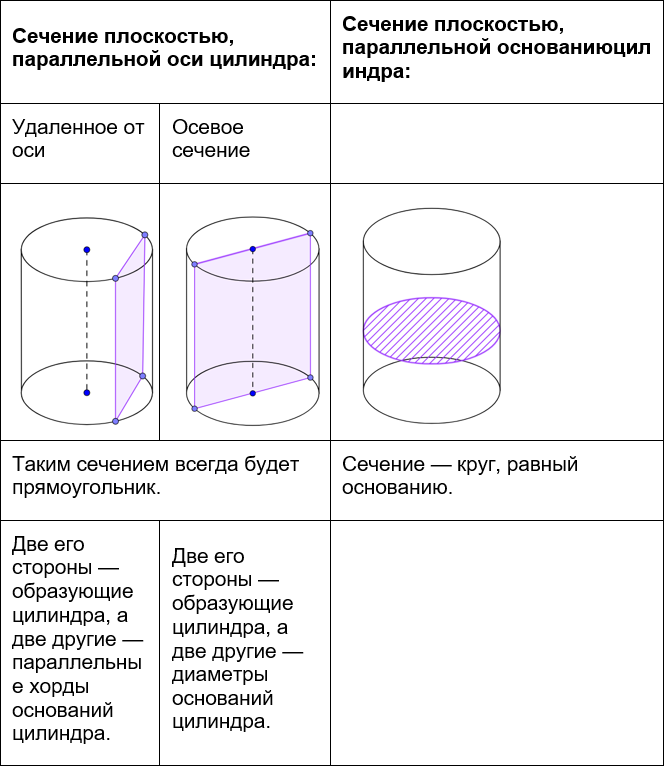
Другие варианты сечений (сечение - эллипс или часть эллипса):

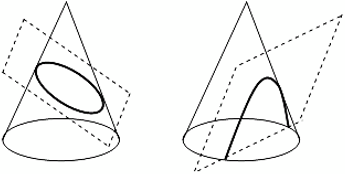
КОНУС
Характерные сечения конуса:

Другие варианты сечений (сечение – эллипс или часть эллипса):
ШАР
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.



 След –прямая l
След –прямая l