Два неравенства являются равносильными, если множества их решений совпадают. При решении неравенств иногда приходится переходить от одного неравенства к другому, более простому. Рассмотрим несколько равносильных переходов: для решения иррациональных, показательных, логарифмических неравенств, неравенств с модулем, дробно-рациональных неравенств.

1. Равносильные переходы для решения иррациональных неравенств

Для избавления от радикалов в иррациональных неравенствах требуется умение возводить обе части неравенства в соответствующую степень. Однако нужно быть осторожными при возведении в четную степень, если хотя бы одна из частей неравенства отрицательная. Неосторожное возведение в квадрат неравенства может повлечь за собой приобретение или потерю решений.

Корни четной степени извлекаются только из неотрицательных чисел, это непосредственно относится к возведению корня четной степени 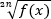в соответствующую четную степень, после чего 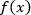стоит уже не под корнем, а значит, лишено неявного ограничения 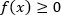. Следовательно, это неявное ограничение мы должны учесть, однако, учитываем мы его для меньшего подкоренного выражения (т.к. для большего это ограничение выполнится автоматически).

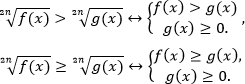
Пример. Решите неравенство

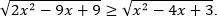
Решение. Применим равносильный переход:

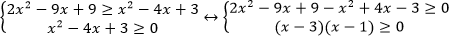
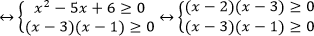
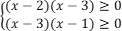
Видим, что решением системы является промежуток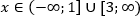

Ответ: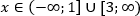

Встречаются такие неравенства, в которых корень сравнивают с выражением. Тогда тоже пользуемся возведением в квадрат для избавления от иррациональности, однако, накладываем дополнительное ограничение – неотрицательность выражения, поскольку значение корня четной степени – число неотрицательное.

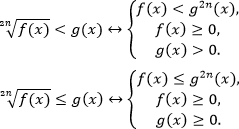
Пример. Решите неравенство

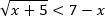
Решение.

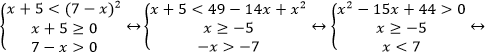
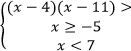
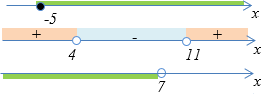
Ответ: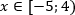

Если иррациональность больше выражения, тогда нужно рассмотреть два случая: выражение может быть неотрицательным или отрицательным. Эти случаи нужно объединить. Поэтому используется совокупность двух систем. Один из двух случаев похож на предыдущую равносильность: тоже возводим в квадрат и добавляем условия. В другом случае рассматриваем только ОДЗ, так как корень всегда больше отрицательного числа.

Получаем следующие равносильные переходы:

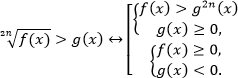
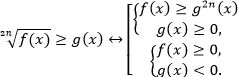
Пример. Решите неравенство

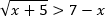
Воспользуемся равносильным переходом.

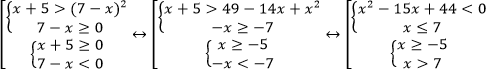
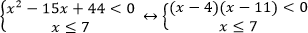
Решением первой системы является полуинтервал (4;7]

Решением второй системы является открытый луч (7;∞).

Значит, решением совокупности является открытый луч (4;∞).

Ответ: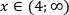

Если неравенство с корнями нечетной степени, то таких ограничений на неотрицательность подкоренного выражения и на значение корня не возникает, поэтому в таком случае просто возводим обе части неравенства в соответствующую нечетную степень.

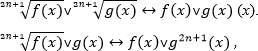
где символ ˅ заменяет один из знаков: <, >, ≤, ≥.

Пример. Решите неравенство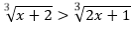

Решение. Воспользуемся равносильным переходом:

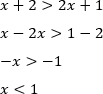
Ответ :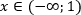

2. Равносильные переходы для решения показательных неравенств

Стандартный способ решения простейших показательных неравенств основывается на монотонности показательной функции, из которой получается следующее основное правило отбрасывания оснований:

Пусть 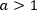, тогда неравенство 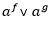равносильно неравенству .

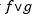В этом правиле последнее неравенство имеет тот же знак, что и первое, т.к. показательная функция с основанием 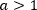возрастает.

Пример. Решите неравенство: .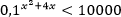

Решение.

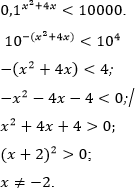
Ответ .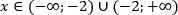

Если же основание 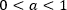, то в сформулированный переход необходимо ввести поправку, поменяв в конце знак на обратный ˄ (т.е. знак > - на знак < и т.д.). Причина смены знака в том, что показательная функция с основанием, меньшим единицы, уже не возрастает, а убывает.

Пример. Решите неравенство: .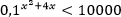

Решение.

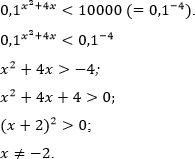
Ответ: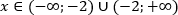

Если неизвестная входит как в основание, так и в показатель степени, то заранее неизвестно, будет ли основание степени больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая. Если неравенство строгое, то получаем следующий равносильный переход:

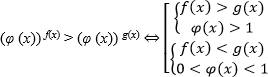
Пример. Решите неравенство

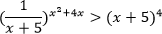
Решение.

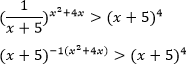
Используем следующий равносильный переход:

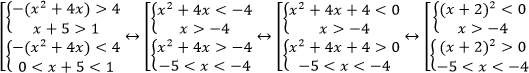
Ответ: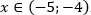

Если неравенство нестрогое, то нужно дополнительно рассмотреть случай – основание равно единице, т.к. тогда получается, что единица в любой степени равна единице, неравенство выполнится. Т.е. получаем следующий равносильный переход:

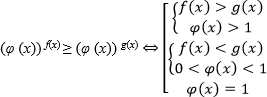
Пример. Решите неравенство:

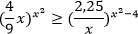
Решение.

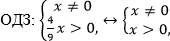
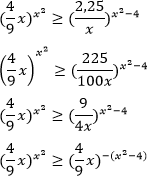
Используем следующий равносильный переход:

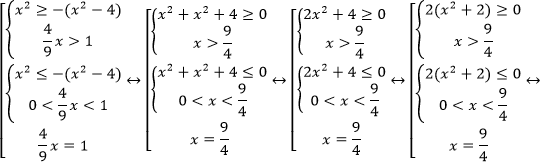
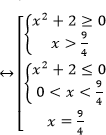
Таким образом, решение неравенства: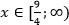

Ответ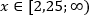

3. Равносильные переходы для решения логарифмических неравенств

Метод решений простейших логарифмических неравенств опирается на монотонность логарифмической функции, т.е. на правило отбрасывания логарифмов. Однако есть отличие от аналогичного правила отбрасывания оснований, которое объясняется тем, что при отбрасывании логарифмов расширяется ОДЗ неравенства. Значит, выражения, стоящие под логарифмами после отбрасывания последних могут стать отрицательными или равными нулю, следовательно, мы должны дополнительно учесть, что подлогарифмическое выражение положительно.

• Если число a > 1, то log_a f (x) > log_a g (x) ⇔ f (x) > g (x) > 0.
• Если число 0 < a < 1, то log_a f (x) > log_a g (x) ⇔ g (x) > f (x) > 0.
• Если число a > 1, то log_a f (x) ≥ log_a g (x) ⇔ f (x) ≥ g (x) > 0.
• Если число 0 < a < 1, то log_a f (x) ≥ log_a g (x) ⇔ g (x) ≥ f (x) > 0

Если неизвестная входит как в основание, так и под знак логарифма, то заранее неизвестно, будет ли основание больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая.

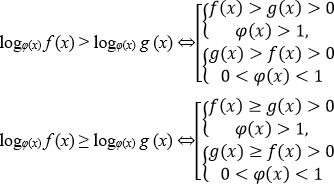
Пример. Решите неравенство

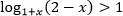
Решение.

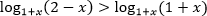
Воспользуемся равносильным переходом:

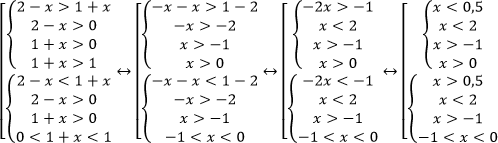
Решением первой системы является интервал (0;0,5)

При решении неравенств второй системы видим, что пересечений решений нет.

Таким образом, решением совокупности является интервал (0;0,5)

Ответ: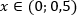

Пример. Решите неравенство

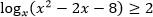
Решение.

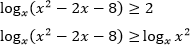
Воспользуемся равносильным переходом:

,

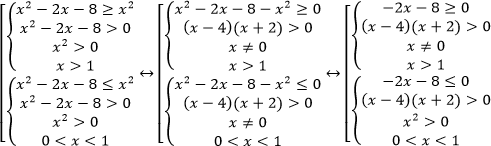
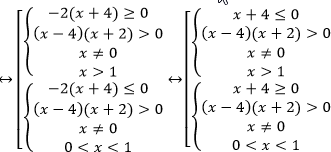
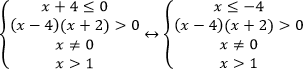видим, что для указанной системы нет решений, т.к. и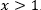

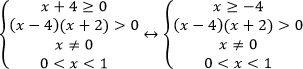
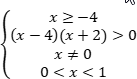
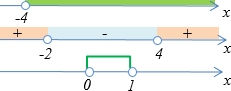
При нанесении решений каждого неравенства системы на числовую прямую видим, что пересечений решений нет. Значит, неравенство не имеет решений.

Ответ: решений нет.

4. Равносильные переходы для решения неравенств, содержащих знак модуля

Если модуль меньше функции, то избавляемся от модуля, но взамен получаем систему из двух неравенств. Учитываем случаи: если число под модулем положительно и если число под модулем отрицательно:

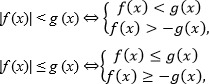
Этот метод работает всегда, даже если выражение 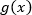отрицательно. Убедимся в этом на примерах.

Пример. Решите неравенство: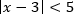

Решение. Воспользуемся равносильным переходом:

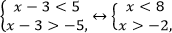
Ответ: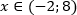

Пример. Решите неравенство: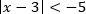

Решение. Воспользуемся равносильным переходом:

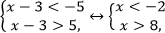
Ответ: решений нет

Рассмотренный пример наглядно демонстрирует, что метод работает всегда. Мы помним, что модуль числа по определению является величиной неотрицательной. В примере модуль меньше отрицательного числа, очевидно, что такое неравенство не имеет решений.

Пример. Решите неравенство

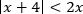
Решение.

Воспользуемся равносильным переходом.

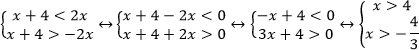
Решением системы является луч (4;∞).

Ответ: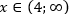

Пример. Решите неравенство

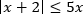
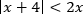
Решение.

Воспользуемся равносильным переходом.

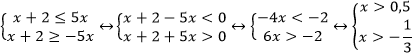
Решением системы является луч (0,5;∞).

Ответ: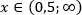

Если модуль больше выражения, то здесь иной равносильный переход.

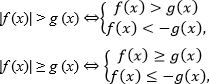
Другими словами, мы рассматриваем два случая: 1) сначала просто игнорируем модуль — решаем обычное неравенство; 2) затем по сути раскрываем модуль со знаком «минус», а затем умножаем обе части неравенства на −1, меня при этом знак. При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.

Пример. Решите неравенство

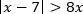
Решение.

Воспользуемся равносильным переходом.

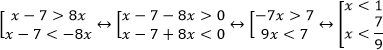
Решением совокупности является луч (-∞;).

Ответ: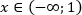

Пример. Решите неравенство

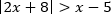
Решение.

Воспользуемся равносильным переходом.

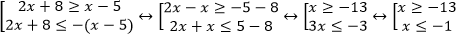
Решением совокупности является луч все множество действительных значений

Ответ: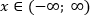

5. Метод расщепления неравенств

Ключевой момент в решении неравенства – преобразование его к виду, в котором левая часть представляет собой произведение каких-либо функций, а правая – равна нулю. Дробно-рациональные неравенства можно привести к равносильной системе:

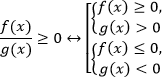
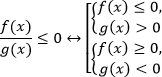
То есть иными словами, дробь положительна, когда числитель и знаменатель одного знака; дробь отрицательна, когда числитель и знаменатель разных знаков.

Произведение двух множителей равносильно совокупности систем:

То есть иными словами, произведение двух множителей положительно, когда оба множителя одного знака; произведение отрицательно, когда оба множителя разных знаков.

Пример. Решите неравенство

Решение. Воспользуемся равносильным переходом.

Решение первой системы – луч [15;∞)

Решение второй системы – открытый луч (-∞;4).

Значит, решением совокупности является объединение полученных решений, т.е.

Ответ:

Пример. Решите неравенство

Решение. Воспользуемся равносильным переходом.

Решение первой системы – полуинтервал (1;1,5]

Вторая система не имеет решений.

Значит, решением совокупности является

Ответ:

Обобщим все рассмотренные методы.