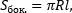5. Стереометрия
 Читать 0 мин.
Читать 0 мин.
5.1. Основные стереометрические фигуры
Среди огромного множества объемных фигур можно выделить три большие группы:

ПРИЗМЫ:
n-угольная призма - многогранник, две грани которого равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней − параллелограммы.
Примеры:
|
|
|
|
|
Треугольная призма |
Четырехугольная призма |
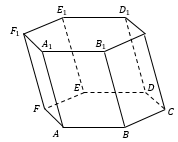
Шестиугольная призма |
Элементы призмы:
|
|
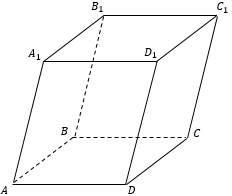
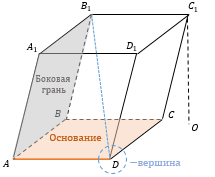
Два n − угольника являются основаниями призмы (ABCD), параллелограммы − боковыми гранями (AB B₁A₁). Стороны граней называются ребрами призмы (например, AD), а концы ребер − вершинами призмы (например, D). Высота призмы - отрезок перпендикуляра, заключенный между основаниями призмы (СO). Для наклонной призмы высота может находится за пределами призмы или лежать внутри нее. Диагональ призмы - отрезок, соединяющий две вершины оснований, не лежащие в одной грани (например, B₁D) |
Виды призм:
|
Прямая призма – призма, боковые ребра которой перпендикулярны плоскостям оснований. |
Наклонная призма – призма, боковые ребра которой являются наклонными к плоскостям оснований. |
|
|
|
Правильная призма - прямая призма, основанием которой является правильный многоугольник.
Свойства призмы:
- Верхнее и нижнее основания призмы – это равные многоугольники.
- Боковые грани призмы имеют вид параллелограмма.
- Боковые ребра призмы параллельные и равны.
- Объем призмы равен произведению площади основания призмы, на высоту.
|
Для прямой призмы высотой будет является любое из боковых ребер. |
|
|
|
|
|
|
|
- Площадь полной поверхности призмы равна сумме площади её боковой поверхности и двойной
площади основания.
|
|
Площадь боковой поверхности прямой призмы:
где P — периметр перпендикулярного сечения, h — высота. То есть:
|
Особенные призмы:
Параллелепипед - призма, все грани которой − параллелограммы.
Прямой параллелепипед - параллелепипед, боковые ребра которого перпендикулярны плоскостям оснований.
|
|
|
|
Прямоугольный параллелепипед - прямой параллелепипед, основанием которого является прямоугольник. Все грани – прямоугольники. |
Куб (гексаэдр) - прямоугольный параллелепипед с равными ребрами. Все грани − квадраты. |
|
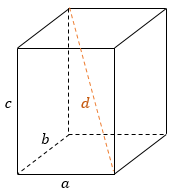
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений: d² = a² + b² + c², где a, b, c − длины ребер, выходящих из одной вершины, d − диагональ параллелепипеда. |
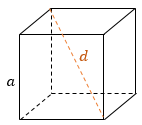
Квадрат диагонали куба равен квадрату его ребра, умноженному на 3: d² = 3a², где a − длина ребра куба. Площадь поверхности куба можно найти по формуле: S = 6a² |
|
Объем прямоугольного параллелепипеда находят по формуле V = abc |
Объем куба можно найти по формуле: V = a³ |
ПИРАМИДЫ:
n-угольная пирамида – многогранник, одна грань которого – n-угольник, а остальные грани − треугольники с общей вершиной.
Примеры:
|
|
|
|
|
Треугольная пирамида |
Четырехугольная пирамида |
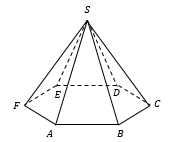
Шестиугольная пирамида |
Элементы пирамиды:
|
|
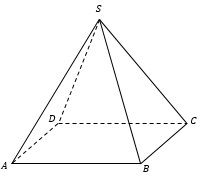
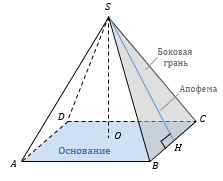
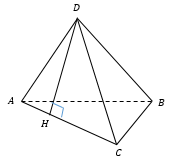
n-угольник называется основанием пирамиды (ABCD), а треугольники − боковыми гранями (например, SBC). Высота пирамиды - отрезок перпендикуляра, проведенного из вершины пирамиды к плоскости основания (SO). Для абсолютно произвольной пирамиды положение точки O заранее неизвестно. Апофема - высота боковой грани правильной пирамиды, проведенная из её вершины (SH). |
Особенные пирамиды:
Правильная пирамида – пирамида, основанием которой является правильный многоугольник, а высота опускается в центр вписанной и описанной окружности многоугольника, лежащего в основании пирамиды. В правильной пирамиде обязательно равны между собой ребра основания, и равны между собой боковые ребра. Но не обязательно боковое ребро равно ребру в основании.
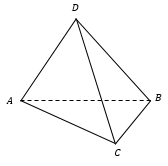
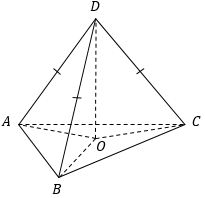
Тетраэдр - треугольная пирамида. Тетраэдр называется правильным, если все его ребра равны.
Усеченная пирамида – многогранник, вершинами которого служат вершины основания пирамиды и вершины её сечения плоскостью, параллельной основанию пирамиды. Основания усеченной пирамиды − подобные многоугольники.
Свойства пирамиды:
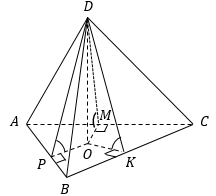
- Если все боковые ребра пирамиды равны или наклонены к плоскости основания под одним и тем же углом, то высота опускается в центр описанной окружности.
- Если боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом (двугранные углы при основании равны), то высота опускается в центр вписанной окружности.
|
|
|
|
Если О – центр вписанной окружности |
Если О – центр описанной окружности |
- Объем пирамиды равен произведению площади ее основания на высоту, деленному на три:
|
|
|
- Площадь полной поверхности пирамиды складывается из площади основания и суммы площадей всех боковых граней (при этом для произвольной пирамиды эти грани могут быть разные, поэтому площади у них тоже будут разные).
Площадь боковой поверхности правильной пирамиды можно найти по одной формуле

где  — периметр основания,
— периметр основания, 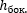 — апофема пирамиды.
— апофема пирамиды.
|
|
Если ABCD — произвольная пирамида, то
Если ABCD — правильная пирамида, то
|
ТЕЛА ВРАЩЕНИЯ:
Цилиндр – фигура, полученная в результате вращения прямоугольника вокруг одной из его сторон.
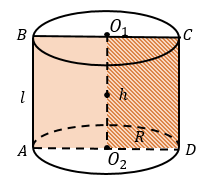
Элементы цилиндра:
|
|
l (AB, CD) – образующая ABCD − осевое сечение цилиндра, полученного вращением прямоугольника |
Свойства цилиндра:
Любое сечение цилиндра, параллельное его основанию – круг, равный основанию цилиндра. Сечение цилиндра, наклонное к его оси и основанию – эллипс.
где
Боковая поверхность равна:
где R − радиус основания, h − высота, l − образующая цилиндра. |
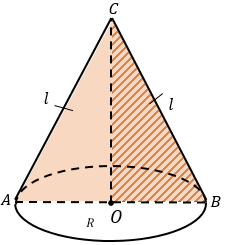
Конус – фигура, полученная в результате вращения прямоугольного треугольника вокруг одного из катетов.
Элементы конуса:
|
|
OС − ось вращения и высота l (AC, CB) – образующая ABC − осевое сечение конуса, полученного вращением треугольника ABC вокруг его стороны OС |
Свойства конуса:
Любое сечение конуса, параллельное его основанию – круг, подобный основанию конуса. Сечение конуса, наклонное к его основанию и не проходящее через вершину – эллипс.
где
Боковая поверхность равна:
где R − радиус основания, l − образующая конуса. |
Сфера – фигура, полученная в результате вращения полуокружности вокруг ее диаметра.
Шар – фигура, полученная вращением полукруга вокруг его диаметра.
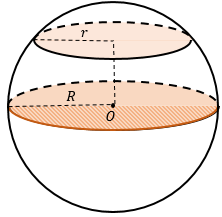
Свойства шара и сферы:
|
|
Сечение шара плоскостью, проходящей через его центр, называется большим кругом (круг радиуса R).
|


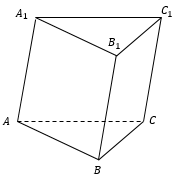
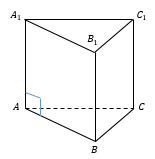
 – прямая треугольная призма
– прямая треугольная призма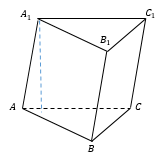
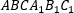 – наклонная треугольная призма
– наклонная треугольная призма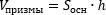
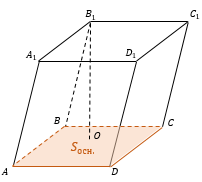
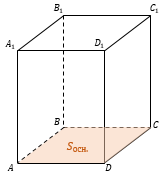
 — произвольная призма.
— произвольная призма.
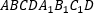 — прямая призма.
— прямая призма.


 - прямая призма.
- прямая призма.
 то
то ,то
,то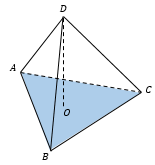
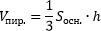
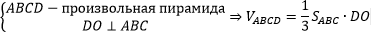
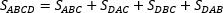

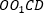 вокруг его стороны
вокруг его стороны 

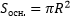 – площадь основания цилиндра; h – высота.
– площадь основания цилиндра; h – высота.


 – площадь основания конуса; h – высота.
– площадь основания конуса; h – высота.