4. Планиметрия
 Читать 0 мин.
Читать 0 мин.
4.7. Комбинации с окружностью
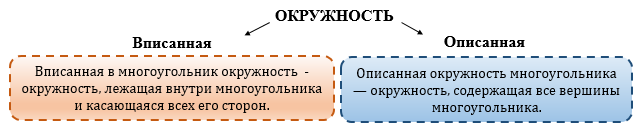
Около выпуклого многоугольника можно описать окружность или в него можно вписать окружность.
|
ТРЕУГОЛЬНИК |
|
|
|
|
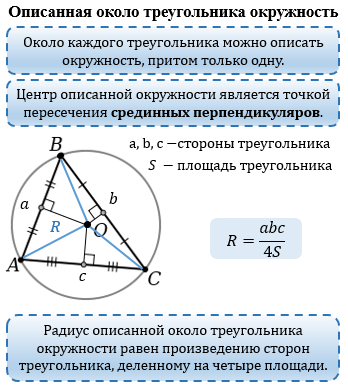
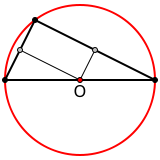
Свойства центра описанной окружности треугольника:
|
|
|
|
|
Остроугольный |
Тупоугольный |
Прямоугольный |
|
У остроугольного треугольника центр описанной окружности лежит внутри треугольника. |
У тупоугольного треугольника центр описанной окружности лежит вне треугольника. |
У прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы. |
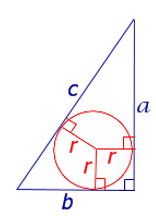
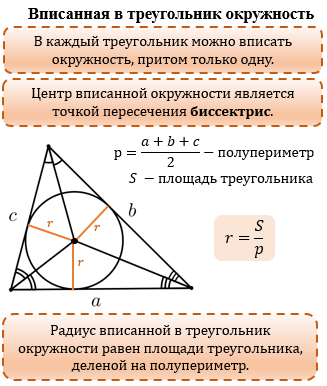
Радиус окружности, вписанной в прямоугольный треугольник с катетами а, b и гипотенузой с, равен:
r = (a + b – c)/2.
|
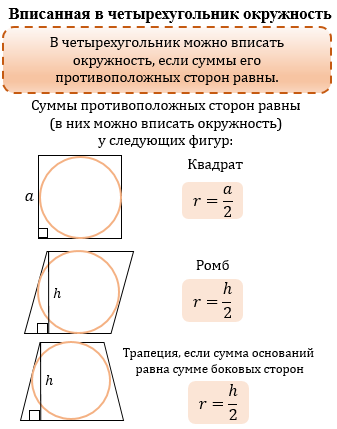
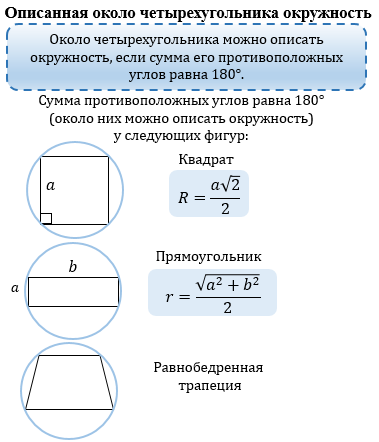
ЧЕТЫРЕХУГОЛЬНИК |
|
|
|
|