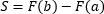3. Алгебра
Читать 0 мин.
3.8. Первообразная
Определение первообразной.
Функция F(x) называется первообразной для функции f(x), если для всех x выполняется равенство:
F'(x) = f(x)
То есть первообразная функции – это функция, от которой взяли производную и получили .
Например:
- Функция F(x) = х² является одной из первообразных* для функции f(x) = 2х, так как
F'(x) = (х²)' = 2x = f(x)
- Функция F(x) = х³+6 является одной из первообразных для функции f(x) = 3х², так как
F'(x) = (х²)' = 3х² = f(x)
* - Фраза «одна из первообразных» предполагает, что у одной из функций есть несколько первообразных. Например, для функции f(x) = 2х первообразными являются функции F(x) = х², F(x) = х²+5, F(x) = х²+17, и множество других. Их общий вид записывается как F(x) = х² + C, а C называются константой интегрирования.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПЕРВООБРАЗНОЙ
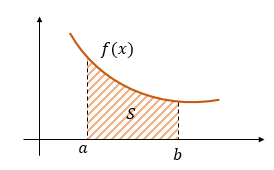
Пусть имеется график функции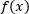 
На оси ОХ отмечены две точки a и b, и через них проведены две прямые до пересечения с графиком Требуется найти площадь, ограниченную графиком 
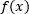осью OX и прямыми x = a и x = b (на рисунке).
Эта площадь будет считаться как определенный интеграл от функции 
.
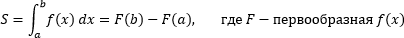
Таким образом, если нам заранее известен явный вид первообразной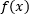 
(то есть 
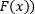), то просто нужно сделать ряд простых шагов, чтобы найти площадь S:
1. Подставить в первообразную левую точку (b) и вычислить ее значение в этой точке – F(b).
2. Подставить в первообразную правую точку (a) и вычислить ее значение в этой точке - F(a).
3. Вычислить F(b) - F(a) (из значения первообразной в левой точке вычитаем значение первообразной в правой точке).
