Неравенства используются для сравнения чисел и выражений. Можно сравнивать числа и делать вывод об их расположении на числовой прямой. Неравенство 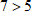означает, что 7 лежит правее на координатной оси.

Так же можно сравнивать самые разные выражения, например, 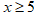или 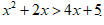В таком случае говорят о множестве решений неравенства, то есть о всех значениях переменной, для которой данное неравенство выполняется (в некоторых случаях это множество может состоять из одной точки или вообще быть пустым).

Неравенства можно обозначать четырьмя способами:

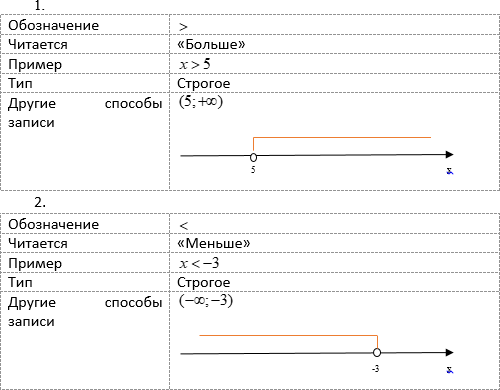
Если неравенство строгое, то граничная точка в решение не входит (поэтому ее «выкалывают» на координатной оси). У нестрого неравенства граничная точка в решение входит.

Правила преобразований неравенств

1. Любое слагаемое в неравенстве можно перенести из одной части уравнения в другую, изменив его знак на противоположный:

2. Можно умножать и делить левую и правую части уравнения на одно и то же положительное число:

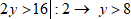
3. Можно умножать и делить левую и правую части уравнения на одно и то же отрицательное число, заменяя при этом знак неравенства на противоположный:

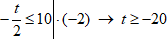
4. Как и в уравнениях можно раскрывать скобки и упрощать выражения в обеих частях или, наоборот, раскладывать на множители.

Решение линейных неравенств

Рассмотрим пример:

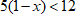
1. С помощью разрешенных преобразований преобразуем неравенства так, чтобы с одной стороны было только выражение, содержащее переменную, а с другой только число:

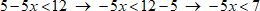
2. Делим на коэффициент перед переменной, при необходимости меняя знак на противоположный:

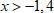
Ответ: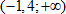

Решение рациональных неравенств других степеней

Для решения таких неравенств применяется метод интервалов. Рассмотрим его алгоритм.

1. Переносим все слагаемые влево.

2. Раскладываем левую часть на множители.

3. Отмечаем на координатной оси нули числителя и знаменателя. Нули знаменателя всегда «выколотые» точки.

4. Определяем знак неравенства в крайнем правом промежутке (можно подставить пробную точку из каждого промежутка в преобразованное неравенство).

5. Определяем знаки в остальных промежутках, двигаясь влево. Если корень имеет нечетную кратность (то есть встречается нечетное число раз), то при переходе через него знак неравенства меняется. В случае четной кратности (корень встречается четное число раз), знак неравенства остается тем же.

6. Выбираем нужные промежутки и записываем ответ.

На практике решение выглядит следующим образом:

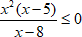
3. Так как пункты 1 и 2 алгоритма уже выполнены, сразу переходим к пункту 3.

Нули числителя: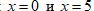

Нули знаменателя: .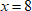

4. Отмечаем полученные точки на координатной прямой.

5. В крайнем правом промежутке можно рассмотреть точку 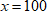. После подстановки получаем, что выражение больше 0.

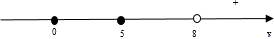
6. Определяем знаки в оставшихся промежутках. Так как корни 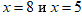встречаются один раз, то при переходе через них знак неравенства меняется. Корень 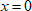имеет кратность два, поэтому знак неравенства сохранится.

7. Так как необходимо определить, когда выражение меньше или равно нуля, то решением является множество 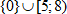. Обратите внимание, что точка 0 является решением, так как неравенство нестрогое.

Ответ: