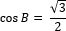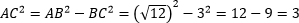4. Планиметрия
 Читать 0 мин.
Читать 0 мин.
4.8. Тригонометрия в геометрии
Решающую роль в решении задач на тригонометрию играет знание определений тригонометрических функций.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ:
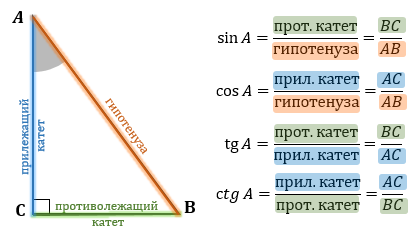
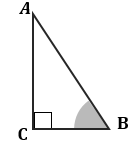
Рассмотрим прямоугольный треугольник ABC и угол A в нем.
|
|
Синус угла — отношение противолежащего катета к гипотенузе. Косинус угла — отношение прилежащего катета к гипотенузе. Тангенс угла — отношение противолежащего катета к прилежащему. Котангенс угла — отношение прилежащего катета к противолежащему. |
НАХОЖДЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ:
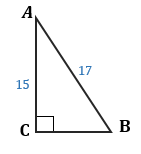
В треугольнике ABC c углом С, равным 90°, гипотенуза AB = 17, а катет AC = 15.
Найдем синус угла B.

Чтобы найти косинус угла B, необходимо значение прилежащего катета — BC, которое нам пока неизвестно. Из Пифагоровой тройки 8 : 15 : 17 находим BC = 8.
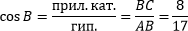
Найдем тангенс угла B.
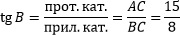
Найдем котангенс угла B.
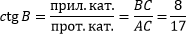
Найдем синус угла A.
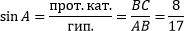
Заметим, что
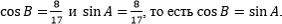
Аналогично можно сказать, что
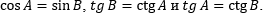
Можно запомнить эту закономерность. Это происходит, потому что ∠A + ∠B = 90° и тут вступают в силу формулы приведения, которые более подробно будут в дальнейшем разобраны на курсе.
ТРИГОНОМЕТРИЧЕСКИЕ ФУКНЦИИ — БЕЗРАЗМЕРНЫЕ ВЕЛИЧНЫ:
Важно понимать, что тригонометрические функции — это безразмерные величины (не имеют единиц измерения), они показывают только отношение.
К примеру, если для треугольника ABC известно, что 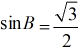 , это не значит, что противолежащий углу B катет AC равен √3, а гипотенуза AB равна 2. Это значит, что противолежащий катет AC относится к гипотенузе AB как √3 к 2. И если бы нам была известна одна из длин: либо катет AC, либо гипотенуза AB — то, зная синус угла B, мы могли бы найти вторую сторону.
, это не значит, что противолежащий углу B катет AC равен √3, а гипотенуза AB равна 2. Это значит, что противолежащий катет AC относится к гипотенузе AB как √3 к 2. И если бы нам была известна одна из длин: либо катет AC, либо гипотенуза AB — то, зная синус угла B, мы могли бы найти вторую сторону.
|
|
Пример 1. Решение:
|
|
|
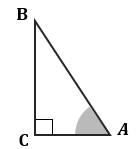
Пример 2. Решение:
Теперь в треугольнике ABC нам известны длины гипотенузы (AB = √12) и катета BC = 3. Воспользуемся теоремой Пифагора и найдем сторону AC. AC = √3 Ответ: √3 |
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ:
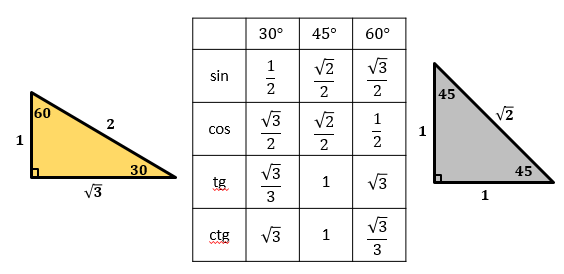
Таблица основных значений тригонометрических функций предлагает значения sin, cos, tg и ctg от нескольких углов: 0°, 30°, 45°, 60°, 90°.
Есть несколько способов нахождения значений тригонометрических функций от табличных углов:
- Учить все значения по таблице. «Зазубривание» — не самый эффективный метод подготовки к экзамену.
- Находить значения по тригонометрическому кругу.
- Воспользоваться «золотым» (с углами 90°, 60° и 30°) и «серебряным» (с углами 90°, 45° и 45°) треугольниками с заведомо известными отношениями сторон.
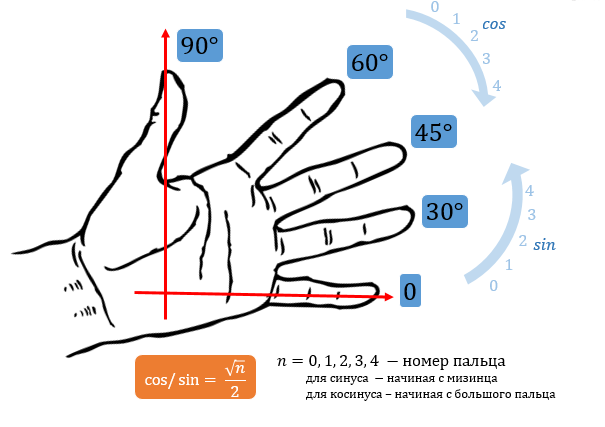
- Правило ладони»
ФОРМУЛЫ, СВЯЗАННЫЕ С ТРИГОНОМЕТРИЧЕСКИМИ ФУКНЦИЯМИ:
1. Основное тригонометрическое тождество:
Основное тригонометрическое тождество — это следствие из теоремы Пифагора для тригонометрического круга. Вот еще один пример получения этой формулы:
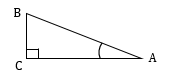
Рассмотрим треугольник ABC. Запишем теорему Пифагора для него:

Поделим каждое слагаемое на AB2.
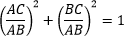
Первое и второе слагаемые — это квадраты синуса и косинуса для угла A или B.
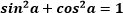
Из основного тригонометрического тождества при наличии значения одной из функций — sin или cos — можно найти вторую.

2. Формулы для тангенса и котангенса.
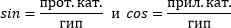
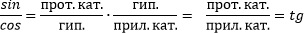
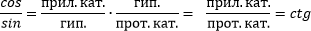
То есть:
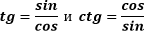
3. Теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
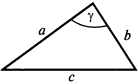
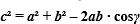
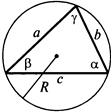
4. Теорема синусов.
Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.
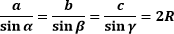


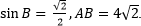 . Найдите сторону AC.
. Найдите сторону AC.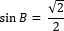
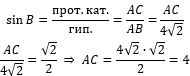
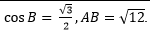 . Найдите сторону AC.
. Найдите сторону AC.