Ключевым моментом в решении систем уравнений является понимание самой сути системы. Система означает, что необходимо учитывать решения нескольких уравнений или нескольких неравенств при записи решения. То есть нужно решить. И первое, И второе уравнение/неравенство, ответом самой системы будет пересечение этих ответов.

Рассмотрим несколько простейших систем.

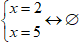
Решением системы являются все значения переменной, при которых выполняются все перечисленные условия. Может ли x одновременно равняться и 2, и 5? Нет, поэтому у этой системы решений нет.

Часто системы усложняются неравенствами.

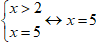
В этой системе требуется, чтобы x был одновременно и равен 5, и был больше 2. При каких значениях это возможно? Только при x =5.

Рассмотрим ещё одну систему:

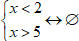
Мы видим 2 отрезка, у которых нет пересечения, поэтому корней данная система не имеет.

Также иногда вам придётся работать с совокупностью. Совокупность предполагает вариативность: может выполняться ИЛИ то, ИЛИ другое условие.

Например:

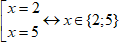
В ответ пойдут обе точки: и 2, и 5. Обратите внимание, что если у нас в ответе конечное количество точек, то их принято писать в фигурных скобочках.

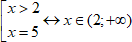
Там подходят или 5, или те x, которые больше 2. Но 5 больше 2, значит, нам просто подходит промежуток от 2 до бесконечности.

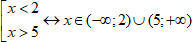
Здесь мы будем рассматривать объединение: если x является корнем хотя бы одного уравнения, неравенства из совокупности, значит, он уже является решением.

Но и это ещё не всё. Иногда совокупность включает в себя систему или система включает себя совокупность. Давайте посмотрим.

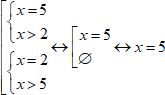
Такая ситуация называется «совокупность двух систем». То есть в ответ пойдут все x, которые удовлетворяют первой системе, и все x, которые удовлетворяют второй системе. Поэтому для того чтобы её решить, нужно сначала решить внутренние системы, а затем в ответ написать все полученные в них корни.

Следующий пример немного другой:

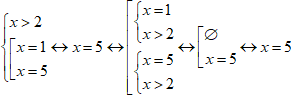
Итак, у нас есть система. Это означает, что должно выполняться 2 условия:

1. x должен быть больше 2.

2. x должен быть равен либо 1, либо 5.

В таких случаях необходимо рассмотреть каждый корень из второго условия на соответствие первому, то есть перейти к совокупности двух систем.

Методы решения систем

Существует несколько основных методов решения систем:

1. Метод подстановки

2. Метод алгебраического сложения

3. Графический метод решения

4. Метод замены переменной

Рассмотрим их на примере следующей системы:

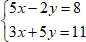
Метод подстановки

1. Выразим y через x из первого уравнения.

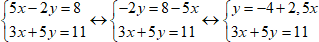
2. Подставим данное выражение вместо y во второе уравнение и решим данное уравнение.

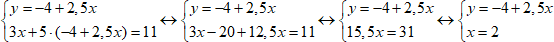
3. Подставим найденное значение x в первое уравнение и найдём y.

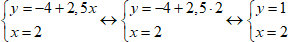
4. Ответ запишем парно.

Ответ: (2; 1).

Метод алгебраического сложения

1. Приведём к такому виду, когда перед одной из переменных в уравнениях стоят равные по модулю коэффициенты, но с противоположными знаками. Например, домножим первое уравнение на 5, а второе – на 2.

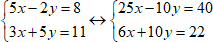
2. Сложим первое уравнение и второе и запишем эту сумму на месте первого уравнения. Второе уравнение оставим неизменным.

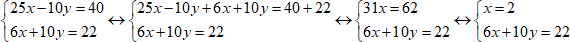
3. Подставим найденное значение x во второе уравнение и найдём y.

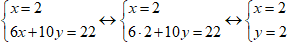
4. Ответ запишем парно.

Ответ: (2; 1).

Графический метод решения

1. Выразим y через x, чтобы к виду уже известных нам функций.

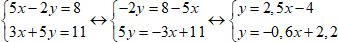
2. Рассмотрим две функции и построим их графики:

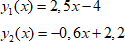
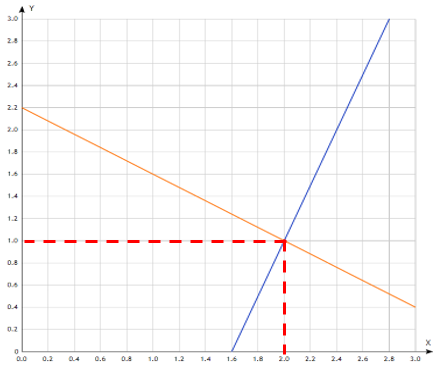
3. Найдём точку пересечения графиков. Видим, что это точка с координатами (2;1).

4. Подставим координаты точки в уравнение и проверим, что равенство выполняется.

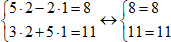
5. Проанализируем монотонность и докажем, что других решений нет.

Функция 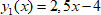монотонно возрастающая.

Функция монотонно убывающая.

Значит, они имеют только одну точку пересечения. Тогда найденная точка является единственным решением.

6. Ответ запишем парно.

Ответ: (2; 1).

Метод замены переменной

Представим, что вместо изначальной системы мы решаем систему вида:

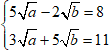
1. Сделаем замену переменных.

Пусть .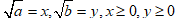

2. Перепишем систему с новыми переменными.

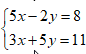
3. Решим систему любым удобным способом.

Получаем ответ (2;1).

4. Вернёмся к исходным переменным.

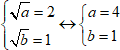
5. Ответ запишем парно.

Ответ: (2; 1).

Таким образом можно решить любое сложное уравнение, если увидеть повторяющиеся элементы и правильно их заменить.

При решении сложных систем уравнений важно мысленно попробовать все способы, чтобы сразу определить наиболее быстрый и правильный путь решения.