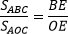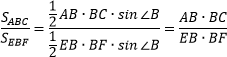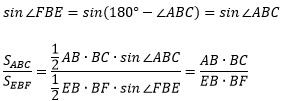Отношения | Планиметрия | Теория | Решутест. Продвинутый тренажёр ЕГЭ

Оглавление

1. Базовая математика

1.1. Делимость 1.2. Числа 1.3. НОК и НОД 1.4. Уравнения в целых числах 1.5. Вероятность 1.6. Прогрессии

Прочитано 0%

2. Текстовые задачи

2.1. Экономические задачи 2.2. Математическая модель 2.3. Текстовые задачи на движение 2.4. Текстовые задачи на производительность

Прочитано 0%

3. Алгебра

3.1. Неравенства 3.2. Рациональные уравнения 3.3. Разложение на множители. Формулы сокращённого умножения 3.4. Степени и корни 3.5. Правила дифференцирования 3.6. Графики функций 3.7. Смысл производной 3.8. Первообразная 3.9. Логарифмические уравнения 3.10. Тригонометрический круг 3.11. Формулы тригонометрии 3.12. Тригонометрические уравнения II 3.13. Простейшие тригонометрические уравнения 3.14. Иррациональные уравнения 3.15. Показательная функция 3.16. Отбор корней 3.17. Уравнения с модулем 3.18. Метод рационализации 3.19. Системы уравнений 3.20. Равносильные системы

Прочитано 0%

4. Планиметрия

4.1. Углы и параллельные прямые 4.2. Векторы 4.3. Треугольники 4.4. Параллелограммы 4.5. Трапеция 4.6. Окружнoсть 4.7. Комбинации с окружностью 4.8. Тригонометрия в геометрии 4.9. Отношения

Прочитано 0%

5. Стереометрия

5.1. Основные стереометрические фигуры 5.2. Углы 5.3. Введение в стереометрию 5.4. Сечения 5.5. Расстояния

Прочитано 0%

4.9. Отношения

Зачастую в геометрических задачах в условии даются отношения отрезков и площадей или отношение отрезков нужно найти. Существует ряд теорем и свойств фигур и их элементов, в которых так или иначе используются отношения.

ОТНОШЕНИЯ ОТРЕЗКОВ:

1. Все медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины: AO : AM = 2 : 1.

2. Средняя линия треугольника равна половине основания: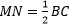

3. Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна ее половине

4. Диагонали параллелограмма точкой пересечения делятся пополам.

Произвольный параллелограмм или ромб:

АО = ОС, BO = OD

Прямоугольник или квадрат:

АО = ОС = BO = OD

ОТНОШЕНИЯ ПЛОЩАДЕЙ:

1. Медиана разбивает треугольник на два равновеликих (по площади) треугольника: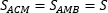

2. Треугольник делится тремя медианами на шесть равновеликих треугольников:

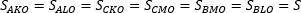
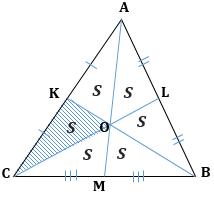
3. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна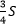

ЛЕММЫ О ПЛОЩАДЯХ ТРЕУГОЛЬНИКА:

Лемма 1

Площади подобных фигур относятся как квадрат коэффициента подобия.

Лемма 2

Если стороны треугольников с общей вершиной лежат на одной прямой, то их площади относятся как основания.

Лемма 3

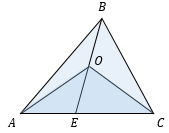
Если два треугольника имеют общую сторону, то их площади соотносятся как длины отрезков BE и OE.

Лемма 4

Если два треугольника имеют общий угол, то их площади соотносятся как произведения соответствующих сторон, прилежащих к этому углу.

Продолжение леммы 4:

Лемма 4 применима даже в том случае, если точки нового треугольника были взяты не на сторонах, а на продолжениях сторон. Пусть точка Е лежит на продолжении стороны AB за вершину В.