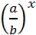3. Алгебра
 Читать 0 мин.
Читать 0 мин.
3.15. Показательная функция
|
a > 0 , b > 0; a0 = 1, 1x = 1;
a−x = ax · ay = ax+y;
(ax)y = axy; ax · bx = (ab)x;
|
Функцию вида f (x) = aˣ, где a > 0 и a ≠ 1, называют показательной функцией.
Основные свойства показательной функции f (x) = aˣ:
|
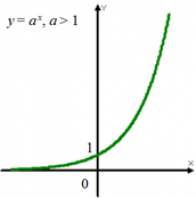
при a > 1 |
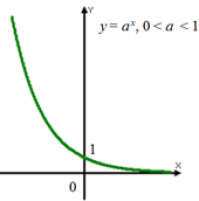
0 < a < 1 |
|
|
Область определения |
D (f) = (−∞; +∞) |
D (f) = (−∞; +∞) |
|
Область значений |
E (f) = (0; +∞) |
E (f) = (0; +∞) |
|
Монотонность |
Возрастает |
Убывает |
|
Непрерывность |
Непрерывная |
Непрерывная |
График показательной функции
Графиком показательной функции является экспонента:
Простейшие показательные уравнения
Показательными называются уравнения, содержащие переменную в показателях каких-либо степеней.
Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
|
Теорема 1. Показательное уравнение af(ˣ) = ag(ˣ) (где a > 0, a ≠ 1) равносильно уравнению f (x) = g (x). |
Простейшее показательное уравнение — это уравнение вида:
ax = b, где а > 0, а ≠ 1. Такое уравнение не имеет корней при b ≤ 0, а при b > 0 имеет единственный корень: x = loga b.
Более сложные показательные уравнения решаются по следующей схеме:
- Перевести все степени к одинаковому основанию. Желательно, чтобы оно было целым и минимальным. Например, вместо 4x лучше писать 2²ˣ, а вместо 0,01x — вообще 10−²ˣ;
- В уравнениях, где есть умножение или деление, надо выполнить эти действия. Помните: при умножении степеней с одинаковым основанием показатели складываются, при делении — вычитаются;
- Если все сделано правильно, получим уравнение вида a f (x) = a g(x), где a — просто число. Его можно отбросить, поскольку показательная функция монотонна. Получим уравнение f (x) = g (x), которое легко решается.
- Помните, что корни — тоже степени, но с дробным основанием:
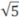 =
= 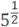 ;
; 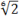 =
= 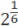 ;
; 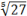 =
= 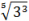 =
= 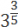 .
.
Задача. Решите уравнение: 4x = 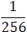 .
.
Решение:
Итак, приведем все степени к основанию 2:
4x = (22)x = 22x; 1 = 20; 256 = 28.
Теперь перепишем исходное уравнение и выполним деление:
4x = 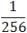
 22x =
22x = 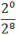
 22x = 20−8
22x = 20−8  22x = 2−8.
22x = 2−8.
Получили простейшее показательное уравнение. Отбрасываем основание — получаем:
2x = −8 ⇒ x = −4.
Ответ: −4.
Задача: Решите уравнение: 92x = 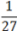 .
.
Решение
Снова приводим все степени к наименьшему целому основанию:
92x = (32)2x = 34x; 1 = 30; 27 = 33.
Обратите внимание: число 27 не является целой степенью девятки. Именно поэтому надо приводить все степени к основанию 3, а не 9. Возвращаемся к исходному уравнению:
92x = 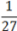
 34x =
34x = 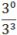
 34x = 30−3
34x = 30−3  34x = 3−3.
34x = 3−3.
Осталось избавиться от основания степени:
4x = −3 ⇒ x = −3/4 = −0,75.
Ответ: −0,75.


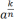 =
= 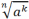 (k ϵ Z, n ϵ N);
(k ϵ Z, n ϵ N); ;
;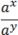 = ax−y;
= ax−y;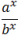 =
=