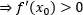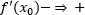3. Алгебра
 Читать 0 мин.
Читать 0 мин.
3.5. Правила дифференцирования
Название производной происходит от слова «произведенная», т.е. образованная от другой величины. Производная характеризует темп изменения функции.
Процесс определения производной какой-либо функции называется дифференцированием. Если говорить совсем просто, то для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию.
ФОРМУЛЫ НАХОЖДЕНИЯ ПРОИЗВОДНЫХ ОСНОВНЫХ ФУНКЦИЙ:
ЧИСЛО, СТЕПЕННАЯ ФУНКЦИЯ, ФУНКЦИЯ С КОЭФФИЦИЕНТОМ

ПРОИЗВОДНАЯ ОТ ПОКАЗАТЕЛЬНО-СТЕПЕННОЙ
И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
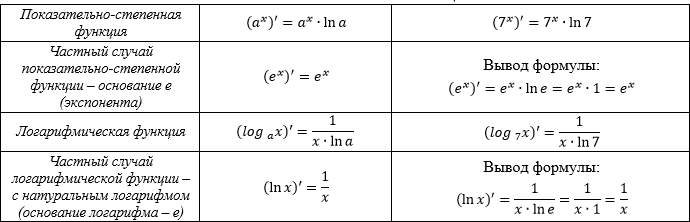
ПРОИЗВОДНАЯ ОТ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ


ПРОИЗВОДНАЯ ОТ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

ПРОИЗВОДНАЯ ОТ СУММЫ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ

СЛОЖНАЯ ФУНКЦИЯ
Сложная функция – это когда внутри функции находится другая функция. То есть аргументом функции является другая функция. Как понять, что функция сложная: если в функции вместо икс стоит что-то другое – это сложная функция.
Например:

Общая формула:

Что она означает: мы берем производную от внешней функции, сохраняя ее аргумент таким, какой он был (то есть сохраняем ту функцию, которая стояла внутри), а потом умножаем ее на производную внутренней функции.
Примеры:


АНАЛИЗ ФУНКЦИЙ
Геометрический смысл производной: значение производной в точке равно тангенсу угла наклона (коэффициент k в уравнении) касательной, проведенной в данной точке.
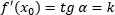
Отсюда можно сделать несколько выводов о том, как можно анализировать функцию с помощью производной:
|
1. Функция возрастает. Если функция возрастает, но наклон касательной, проведенной в любой точке промежутка возрастания будет вправо, значит, ее коэффициент наклона положительный Функция возрастает |
|
2. Функция убывает. Если функция убывает, но наклон касательной, проведенной в любой точке промежутка возрастания будет влево, значит, ее коэффициент наклона отрицательный (k < 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же отрицательна. Функция убывает |
|
3. Экстремум. Точки экстремума, отличаются тем, что в них функция находится в пиковом значении, она и не возрастает, и не убывает. Если провести касательную в точке экстремума, то она будет строго горизонтальна, то есть ее наклон равен 0. А значит, и производная равна 0 (из соотношения между значением производной и коэффициентом наклона касательной выше). Точка экстремума Максимум. До него функция возрастает, после него убывает. В максимуме производная сменяет свой знак с плюса на минус. Максимум: Минимум. До него функция убывает, после него возрастает. В минимуме производная сменяет свой знак с минуса на плюс. Максисмум: |
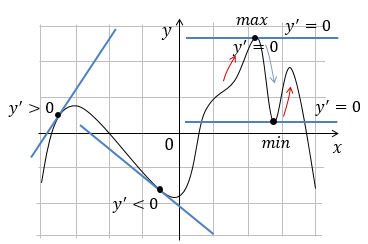
Отсюда можно вывести общий порядок действий при анализе функций:
1. Находим производную от функции.
2. Находим точки экстремума: приравниваем производную к нулю и решаем уравнение.
3. Определяем знаки производной между точками экстремума.
- Если в точке знак производной меняется с плюса на минус – это максимум.
- Если в точке знак производной меняется с минуса на плюс – это минимум.


 . Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же положительна.
. Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же положительна.