

3. Алгебра
 Читать 0 мин.
Читать 0 мин.
3.9. Логарифмические уравнения
Логарифмом числа 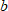 по основанию
по основанию 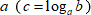 называется такой показатель степени
называется такой показатель степени , в которую нужно возвести
, в которую нужно возвести  , чтобы получить
, чтобы получить 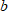 (то есть
(то есть 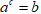 ). При этом задаются ограничения:
). При этом задаются ограничения: 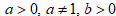 . Значение
. Значение  логарифма может быть любым.
логарифма может быть любым.
Вычислите:
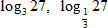
1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.
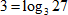
2. При возведении 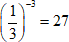 значит,
значит, 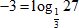
Ответ: 3; -3.
Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.
Пусть 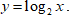 Подставим вместо
Подставим вместо 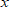 разные числа и определим соответствующие значения переменной
разные числа и определим соответствующие значения переменной 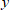 .
.

Отметим координаты точек на плоскости и соединим их плавной линией.
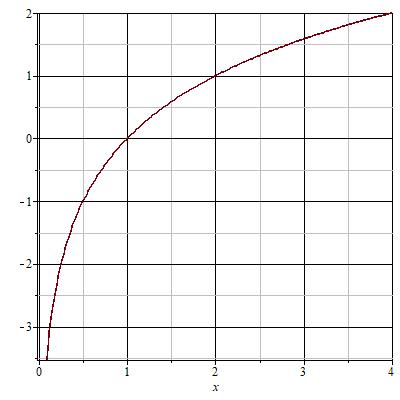
Легко заметить, что функция все время возрастает. Такое поведение характерно для всех логарифмических функций с основанием больше единицы.
Пусть теперь 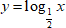 . Составим таблицу значений для этого случая.
. Составим таблицу значений для этого случая.

Тогда график функции будет выглядеть следующим образом.
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.
Графики всех логарифмических функций проходят через точку с координатами (1;0).
Особыми знаками принято обозначать логарифмы с основанием десять 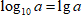 и логарифмы с натуральным основанием
и логарифмы с натуральным основанием 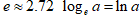 .
.
Свойства логарифмов
Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.


Используем рассмотренные свойства для решения некоторых задач.
Пример 2
Вычислите 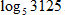
1. Представим 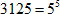 .
.
2. Вынесем степень из—под знака логарифма:
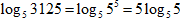
3. Логарифм числа по равному ему основанию равен 1:
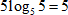
Ответ: 5.
Пример 3
Вычислите 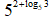
1. Воспользуемся свойством степеней:
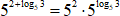
2. Используем основное логарифмическое тождество:
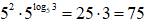
Ответ: 75.
Пример 4
Вычислите 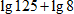
1. Воспользуемся формулой для суммы логарифмов:
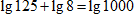
2. Представим 1000 = 103 и вынесем 3 за знак логарифма:
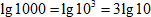
3. Воспользуемся тем, что 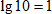 .
.
Ответ: 3.
Пример 5
Вычислить 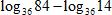 .
.
1. Воспользуемся формулой для частного логарифмов:
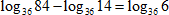
2. Преобразуем основание логарифма 36 = 62 и вынесем, «перевернув», вынесем показатель:
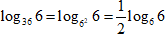
3. Воспользуемся тем, что 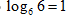
Ответ: 0,5.
Пример 6
Вычислите 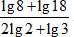 .
.
1. Применим в числителе формулу для сумы логарифмов:
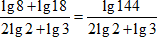
2. В знаменателе внесем 2 под знак логарифма:
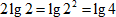
3. Воспользуемся формулой суммы логарифмов для знаменателя:
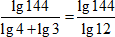
4. Перейдем от частного к логарифму с основанием 12:
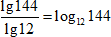
5. Представим144 = 122, вынесем степень за знак логарифма и воспользуемся соотношением 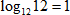
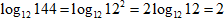
Ответ: 2.
Кроме выражений с числами, на экзамене могут встретиться выражения, содержащие переменные. В этом случае можно использовать те же формулы и правила.
Пример 7
Вычислите 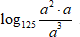
1. Преобразуем отдельно подлогарифмическое выражение:
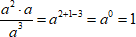
2. Логарифм 1 по любому основанию равен 0:
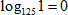
Ответ: 0.






















