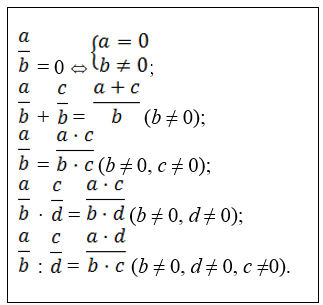3. Алгебра
Читать 0 мин.
3.14. Иррациональные уравнения
Арифметический корень
Пусть n — натуральное число, отличное от единицы, а — неотрицательное число.
Арифметическим корнем n-й степени из неотрицательного числа а называется неотрицательное число, n-я степень которого равна а.
Для арифметического корня n−й степени из неотрицательного числа а, используется обозначение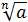 
. Если n = 2, пишут 
.
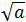По определению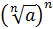
= a.
Для любых, в том числе отрицательных, значений а справедлива формула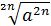 
= │a│, в частности, 
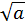= │a│ и
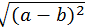=│a − b│.
Свойства арифметического корня
Если a и b — неотрицательные числа, n и k — натуральные числа, отличные от единицы, m — целое число, то имеют место следующие соотношения:
= 
;
= 
· 
;
= 
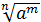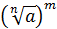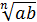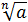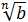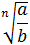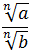, b ≠ 0;
= 
;
· 
= 
;
: 
= 
.
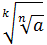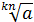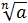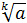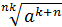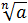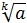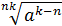Степень с дробным показателем
Если a — положительное число, m — целое число, n — натуральное число и n ≥ 2, то
= 
= 
.
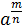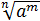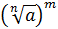Формулы сокращенного умножения
|
Квадрат суммы: Квадрат разности: Кубсуммы: Кубразности: Разность квадратов: Суммакубов: Разность кубов: |
(a + b)² = a² + 2ab + b²; (a – b)² = a² − 2ab + b²; (a + b)³ = a³ + 3a²b + 3ab² + b³; (a + b)³ = a³ − 3a²b + 3ab² − b³; a² − b² = (a – b)(a + b); a³ + b³= (a + b)(a² − ab + b²); a³ − b³ = (а – b)(a² + ab + b²). |
Дробно−рациональные уравнения
Свойства рациональных дробей:
