

3. Алгебра
 Читать 0 мин.
Читать 0 мин.
3.12. Тригонометрические уравнения II
Тригонометрические уравнения части 2 предполагают:
1. Знание тригонометрических формул (основное тригонометрическое тождество и следствия из него, формулы двойного угла, формулы приведения, формулы суммы/разности тригонометрических функций).
2. Умение решать простейшие тригонометрические уравнения (с помощью формул или тригонометрического круга).
Первые два пункта должны быть идеально отработаны, так как станут фундаментом решения сложных заданий.
3. Знание метода разложения на множители и метода замены переменной.
4. Понимание сути однородных уравнений и методов их решения, а также знание других дополнительных методов решения, специфических для тригонометрии.
3. Методы разложения на множители и замены переменной универсальны для всех уравнений с различными видами функций.
Рассмотрим примеры.
Пример 1.
x3 – 5x2 = –6x
Метод разложения на множители
1. Переносим все влево, справа остается 0.
x3 – 5x2 + 6x = 0
2. Если все слагаемые содержат повторяющийся элемент, выносим его за скобку.
x(x2 – 5x + 6) = 0
*В противном случае группируем слагаемые так, чтобы получить повторяющийся элемент или выражение, которое выносим за скобку.
3. Получаем произведение выражений, равное нулю.
Разложим вторую скобку на множители:
x(x – 2)(x – 3) = 0
4. Приравниваем каждое из выражений нулю.
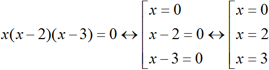
5. В ответ записываем решение всех получившихся уравнений.
Ответ: 0; 2; 3.
Точно также можно решать уравнения, если повторяющийся элемент — тригонометрическая функция.
Пример 2.
sinx – cosx = –sinxcosx + 1
1. Переносим все влево, справа остается 0.
sinx – cosx + sinxcosx – 1 = 0
2. Если все слагаемые содержат повторяющийся элемент, выносим его за скобку.
*В противном случае группируем слагаемые так, чтобы получить повторяющийся элемент или выражение, которое выносим за скобку.
(sinx + sinxcosx) – (1 + cosx) = 0
sinx(1 + cosx) – (1 + cosx) = 0
3. Получаем произведение выражений, равное нулю.
(1 + cosx)(sinx – 1) = 0
4. Приравниваем каждое из выражений нулю.
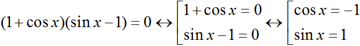
5. Далее решаем полученные простейшие тригонометрические уравнения и записываем ответ.
Пример 3.
sin2x – 6sinx = –5
Метод замены переменной:
1. Видим, что уравнение похоже на квадратное, но вместо аргумента стоит функция, которая зависит от аргумента.
Вводим замену, выделив повторяющийся элемент.
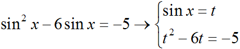
2. Новая переменная должна иметь те же ограничения, что и заменённый элемент.
Записываем дополнительные условия sinx, cosx 
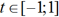
3. Решаем уравнение с новой переменной.
В данном случае решаем квадратное уравнение.
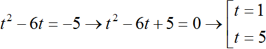
4. Возвращаемся к исходной переменной.
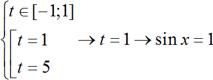
5. Решаем получившиеся простейшие тригонометрические уравнения.
4. Однородные уравнения бывают разные.
Уравнение, в котором все функции стоят в первой степени, а справа стоит 0, называется однородным уравнением первой степени.
Однородные уравнения 1 степени: вида asinx + bcosx = 0
Например, 2sinx + 3 cosx = 0 — однородное уравнение, для решения которого необходимо поделить на одну из представленных функций, например, на cosx.
Важно! В однородных уравнениях мы имеем право делить на cosx, так как знаем, что cosx=0 не является корнем уравнения (в противном случае sinx = 0 тоже было бы корнем уравнения, что противоречит основному тригонометрическому тождеству).
Уравнение, в котором каждое слагаемое — это функция во второй степени или произведение двух функций, а справа стоит 0, называется однородным уравнением второй степени.
Однородные уравнения 2 степени: вида asin2x + bsinxcosx + ccos2x = 0.
Например, sin2x + 3sinxcosx + 2cos2x = 0 — однородное уравнение, для решения которого необходимо поделить на одну из представленных функций, например, на cos2x, для приведения к уравнению, похожему на квадратное.






















