

2. Текстовые задачи
 Читать 0 мин.
Читать 0 мин.
2.2. Математическая модель
Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.
Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.
Пример:
Решение любой текстовой задачи можно разделить на несколько основных этапов:
- Работа с условием
- Составление математической модели
- Проверка ответа
Работа с условием
Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.
Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?
Иллюстрация:
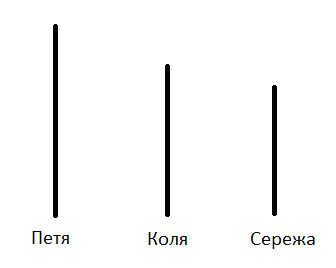
Из рисунка сразу понятен ответ: Петя выше всех.
Пример.
Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?
Иллюстрация:
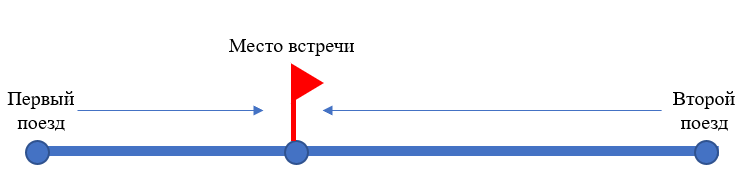
Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.
Составим математическую модель:
45х + 55х = 200
100х = 200
х = 2 ч
Ответ: 2 ч.
Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.
Математическая модель
Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.
x — число девочек
y — число мальчиков
| Реальная ситуация | Математическая модель |
|---|---|
| В классе поровну мальчиков и девочек | $ {\ x=y} $ |
| Девочек на 5 больше, чем мальчиков | $ {\ x=y+5, \; или\; x-y=5,\; или\; x-5=y} $ |
| Мальчиков в 2 раза больше, чем девочек | $ {\ y=2x, \; или\; \frac{y}{2}=x,\; или\; \frac{y}{x}=2} $ |
| Если в класс перейдут 3 мальчика, то девочек станет в два раза больше | $ {\ y=2(y+3)} $ |
Алгебраическая зависимость
Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.
При составлении уравнения особое значение играют используемые предлоги: «в» и «на».
Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?
Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.
Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.
Выразим рост мальчиков.
Петя выше Коли на 20 см: П – 20 = К
Сережа ниже Коли на 10 см: К = С + 10
Подставим в первое уравнение рост Коли: П – 20 = С + 10
Нам нужно найти, на сколько см Петя выше Сережи: П – С
П – 20 = С + 10
П – С = 20 + 10
П – С = 30
Получаем, что Петя выше Сережи на 30 см.
Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?
Решение:
Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.
Маша сделала в два раза больше снежинок, чем Коля: К = М/2
Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4
Вместе ребята сделали 12 снежинок: М + К + Р = 12
Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12
М = 4.
Маша сделала 4 снежинки.
Процентная зависимость
С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?
Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.
Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.
Так что же такое один процент?
Процент — это всегда доля какого-то числа.
100% — все число
50% — половина
25% — четверть
Чтобы найти 1%, необходимо поделить всё число на 100.
Пример:
Есть 100 яблок.
$ \ 1\% \;от \;всех \;яблок\; –\frac{100}{100} = 1 \;яблоко. $
Есть 200 груш
$ \ 1\% \;от \;всех \;груш\; –\frac{200}{100} = 2 \;груши. $
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.
Пример:
200 груш — 100 %
2 груши — 1 %
Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.
$ \frac{200}{2}=\frac{100}{1} $
Исходя из правил работы с дробями, получаем правила работы с пропорцией.
1. Внутри одной дроби можно сокращать значения.
2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100
Эту тему мы еще подробно пройдем на курсе.
Рассмотрим несколько примеров работы с процентами в текстовых задачах.
Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов
Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?
Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек
Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?
Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?
На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:
Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880
Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880
Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.
Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.






















