Тригонометрия пришла людям на помощь, когда выяснилось, что для многих расчетов недостаточно тех углов, которые определялись обычной геометрией. И правда, в геометрии мы не встретим углы больше, чем 360⁰. Ненасытные ученые хотели больше. Поэтому, по сути, тригонометрия – это раздел математики, посвященный углам.

Нарисуем тригонометрический круг.

Алгоритм для создания тригонометрического круга:

• Рисуем системы координат;
• Изображаем круг. Центр совпадает с центром системы координат. Рекомендуется выбирать за длину радиуса 4, 6 или 8 клеточек в зависимости от того, какого размера вы хотите круг.
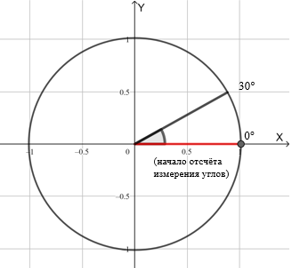
• Ставим точку отсчёта 0 для измерения углов.
• Затем изобразим угол: одну сторону зафиксируем на горизонтальной оси, а другая останется свободной и сможет крутиться, куда вздумает, как на шарнире.

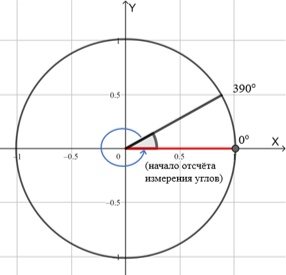
• Теперь мысленно вращаем незакрепленную сторону. Пусть она вращается против часовой стрелки. Вот она совершила полный оборот и вернулась на свое место. Визуально угол остался прежним, но на самом деле к нему добавился полный оборот, то есть 360⁰.
• Учитывая полные обороты, каждый угол можно представить, как

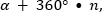где n – целое число

Договоримся, что вращение против часовой стрелки – это положительно направление, а по часовой – отрицательное.

Измерение углов

В математике углы измеряют не только в привычных нам градусах, но и в радианах. Соответствие между ними установить очень просто.

Некоторые углы очень легко определить:

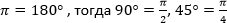
Можно пользоваться формулой: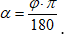

Также есть обратная формула: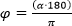

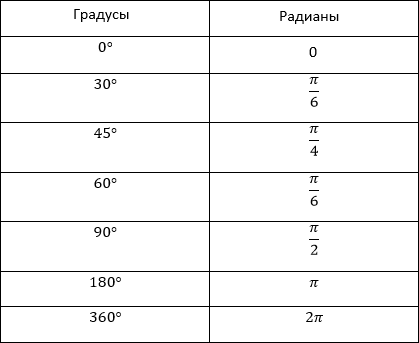
Изображение табличных значений на тригонометрическом круге.

Нарисуем тригонометрический круг.

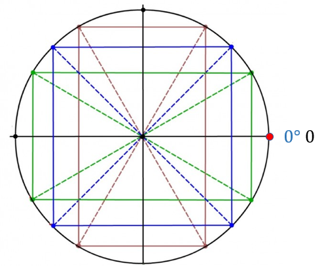
Далее идём по кругу с шагом в 45, то есть, 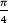. Эти углы делят каждую четверть пополам.

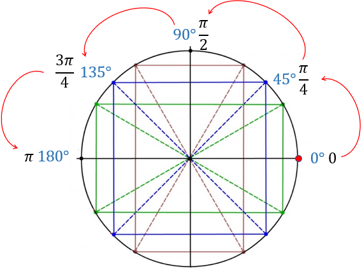
Затем идём по кругу с шагом в 30, то есть, 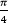, Каждая четверть таким образом делится на 3 равные части.

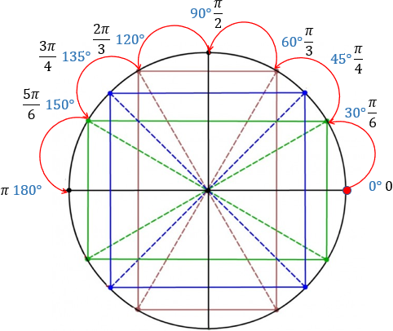
Снизу заполним не большими углами, а отрицательными. То есть, зеркально отразим верхнюю часть круга вниз.

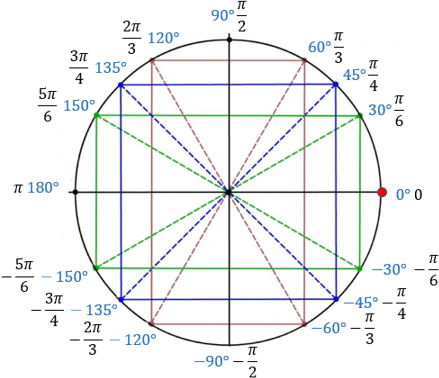
Теперь заполним новый круг, но уже углами от 0 до 2π.

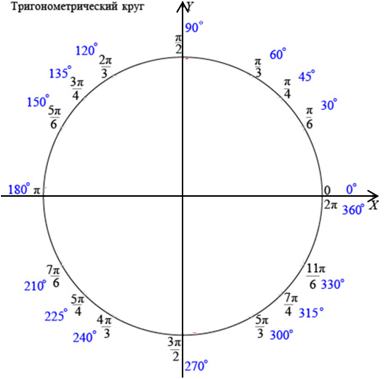
Определение значений тригонометрических функций

С греческого тригонометрия переводится как «измерение треугольника». Именно треугольник дает понимание о том, что же такое тригонометрические функции в окружности. Возьмем прямоугольный треугольник.

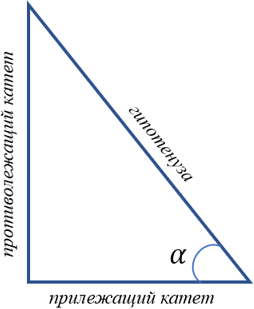
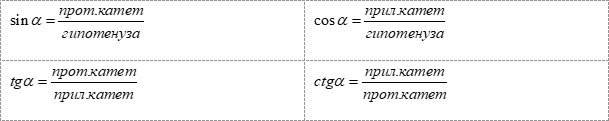
Снова перейдем к окружности. Вставим в нее прямоугольный треугольник так, чтобы гипотенуза совпала с радиусом, который мы будем принимать за 1.

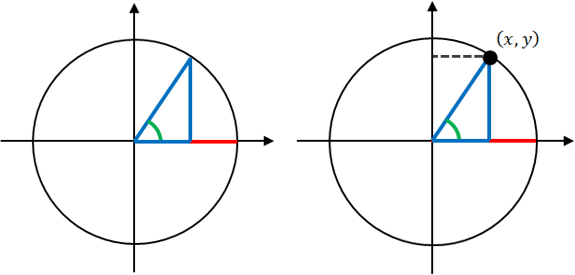
Точка пересечения радиуса с окружностью, как и любая точка в плоскости, имеют свои координаты (x,y). Причем, для отмеченного нами угла противолежащий катет равен y, а прилежащий – x. А теперь немного магии. Заменим на x, y и 1 величины в определении тригонометрических функций.

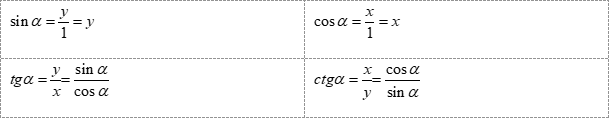
Получается, что косинус – это значения на оси абсцисс, а синус – значения на оси ординат.

Ось тангенсов параллельна оси синусов и проходит через точку с координатой x = 1, ось котангенсов параллельна оси косинусов и проходит через точку y = 1. Соответствующее значение на них получается продлением радиуса до пересечения с одной из осей.