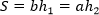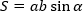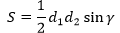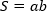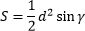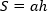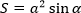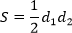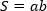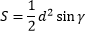4. Планиметрия
 Читать 0 мин.
Читать 0 мин.
4.4. Параллелограммы
Среди произвольных четырехугольников можно выделить два особенных: параллелограмм и трапеция. Параллелограммы можно разделить на:
- произвольный параллелограмм,
- прямоугольник;
- ромб;
- квадрат.
Часто для решения задания достаточно знать определение фигуры и уметь им пользоваться.
Параллелограмм.
Параллелограмм ― это четырёхугольник, у которого противоположные стороны равны и параллельны (АВ || CD, AC || BD).
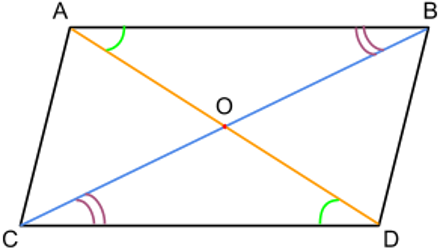
То есть, если у четырехугольника есть хотя бы одна пара равных и параллельных противоположных сторон, то этот четырехугольник – параллелограмм, а значит, все его противоположные стороны равны и параллельны.
Свойства параллелограмма
Из определения параллелограмма вытекает ряд его свойств. Для любого параллелограмма (то есть произвольного и особенного, вроде ромба или прямоугольника) выполняются условия:
1. Противоположные стороны равны (АВ = СD, AC = BD).
2. Противоположные углы равны (∠А = ∠D, ∠B = ∠C).
3. Сумма углов, прилежащих к одной стороне, равна 180°: ∠BAC + ∠ACD = 180°, ∠ABD + ∠BCD = 180° (это вытекает из параллельности противоположных сторон, так как указанные углы являются односторонними).
4. Из параллельности сторон вытекает равенство частей углов (например, ∠DAB = ∠ADC; ∠BCD = ∠ABC как накрестлежащие).
5. Две диагональ делят параллелограмм на две пары равных треугольников ∆ABC = ∆BCD, ∆ABD = ∆ACD (по стороне и двум углам).
6. Диагонали параллелограмма точкой пересечения делятся пополам (АО = OD, CO = OB).
Интересные, но редко применимые свойства параллелограмма:
7. Биссектрисы противоположных углов параллелограмма всегда параллельны.
8. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом.
Признаки параллелограмма
Для того, чтобы в задании с развернутым ответом доказать, что фигура действительно является параллелограммом, нужно знать, какими свойствами мы можем пользоваться. Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон: AB||CD и BC||AD.
2. Четырехугольник имеет пару параллельных и равных сторон: AB||CD, AB = CD (или BC||AD, BC = AD).
3. В четырехугольнике противоположные стороны попарно равны: AB = CD, BC = AD.
4. В четырехугольнике противоположные углы попарно равны: ∠DAB = ∠BCD, ∠ABC = ∠CDA.
5. В четырехугольнике диагонали точкой пересечения делятся пополам: AO = OC, BO = OD.
6. Сумма углов четырехугольника прилегающих к любой стороне равна 180°: ∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°.
Формулы площади параллелограмма
Существую три формулы площади параллелограмма, которые применимы как для произвольного параллелограмма, так и для ромба, прямоугольника, квадрата.
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
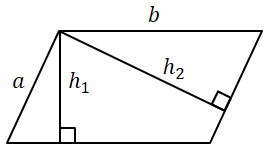
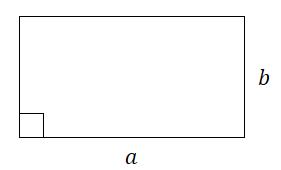
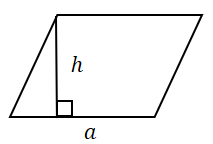
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. |
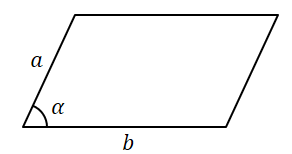
Площадь параллелограмма равна произведению его сторон на синус угла между ними. |
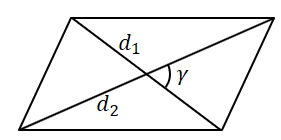
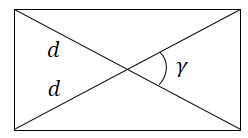
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними. |
Прямоугольник
Прямоугольник ― это параллелограмм, у которого все углы прямые. Для того, чтобы параллелограмм был прямоугольником, достаточно, чтобы хотя бы один его угол был равен 90°, тогда и все остальные будут равны 90°.
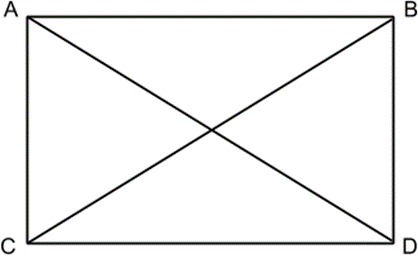
Кроме свойств параллелограмма, у прямоугольника есть и несколько своих:
1. Диагонали прямоугольника равны (AD = BC).
Стороны прямоугольника являются его высотами.
В связи с этими свойствами, формулы площади параллелограмма для прямоугольника можно немного изменить. 1 и 2 формула обращаются в одну, во второй формуле произведение диагоналей можно заменить на квадрат одной диагонали.
|
1 |
2 |
|
|
|
|
|
|
|
Площадь прямоугольника равна произведению его смежных сторон. |
Площадь прямоугольника равна половине произведения квадрата его диагонали на синус угла между диагоналями. |
Ромб
Ромб ― это параллелограмм, у которого все стороны равны. На самом деле, достаточно, чтобы были равны хотя бы две его соседние стороны, тогда все стороны будут равны.
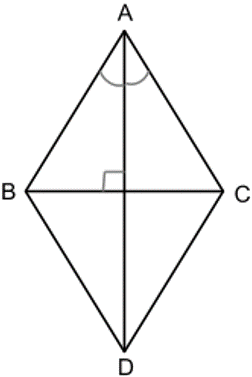
Кроме свойств параллелограмма, у ромба есть несколько своих:
1. Диагонали ромба являются биссектрисами его углов.
2. Диагонали ромба пересекаются под прямым углом (AD ⊥ BC).
То есть, параллелограмм является ромбом, если выполняется хотя бы одно из условий:
- Две его смежные стороны равны;
- Его диагонали пересекаются под прямым углом;
- Одна из диагоналей делит содержащие её углы пополам;
- Все высоты равны.
На основании свойств можно немного изменить формулы площади параллелограмма для ромба:
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
Площадь ромба равна произведению его стороны на высоту (при чем для любой стороны это выражение будет одинаковым, так как стороны равны). |
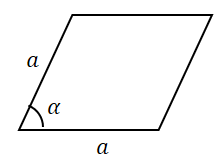
Площадь ромба равна произведению квадрата его стороны на синус угла между сторонами. |
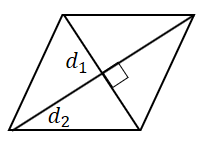
Площадь ромба равна половине произведения его диагоналей. |
Квадрат
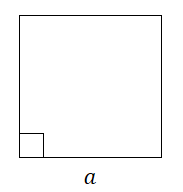
Квадрат ― это параллелограмм, у которого все стороны равны и все углы равны (AB = BC = CD = DA и ∠A = ∠B = ∠C = ∠D = 90°). То есть квадрат сочетает в себе свойства и ромба, и прямоугольника, поэтому ему присущи не только свойства параллелограмма, но и ромба с прямоугольником. Надо запомнить, что любой квадрат является ромбом и прямоугольником, но не любой ромб или прямоугольник является квадратом.
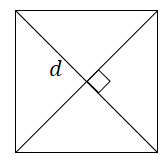
Центры вписанной и описанной окружностей квадрата совпадают и одновременно являются точкой пересечения диагоналей (т. О).
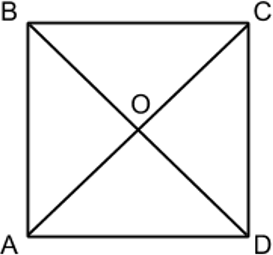
Формулы площади квадрата:
|
1 |
2 |
|
|
|
|
|
|
|
Площадь квадрата равна его стороне, возведенной в квадрат. |
Площадь квадрата равна одной второй квадрата его диагонали. |