

3. Алгебра
 Читать 0 мин.
Читать 0 мин.
3.4. Степени и корни
Для того, чтобы возвести число в степень с натуральным показателем  , нужно умножить число само на себя
, нужно умножить число само на себя  раз:
раз:
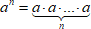
В этой записи  – основание,
– основание,  – показатель степень.
– показатель степень.
Для проведения вычислений удобно использовать формулы преобразования выражений со степенями. Они универсальны и работают для любых показателей (целых, рациональных или иррациональных).
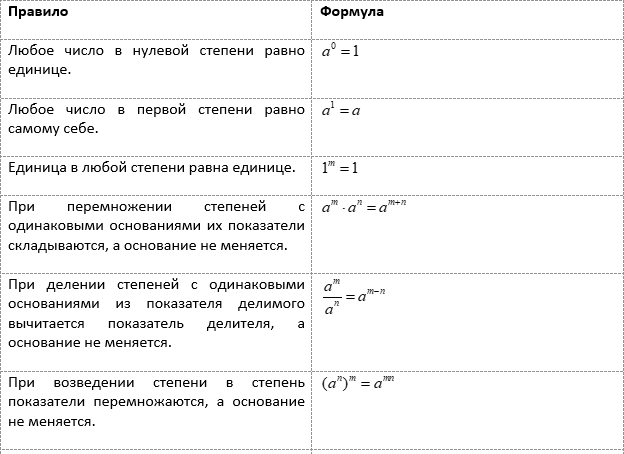

Применим эти правила для решения следующих задач.
Пример 1

Воспользуемся формулой для частного степеней с одинаковыми основаниями.
Пример 2
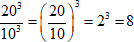
Так как степень частного равна частному степеней, занесем всю дробь под одну степень.
Пример 3

Для удобства представим  и занесем всю дробь под одну степень.
и занесем всю дробь под одну степень.
Иногда для записи дробных степеней используют специальный знак – корень. На самом деле корень - всего лишь дробная степень:

Чаще всего встречается квадратный корень из числа:
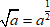
Выражения с корнями преобразуется по тем же правилам, что и все остальные степени.
Следует различать корни нечетной степени 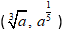 и корни четной степени
и корни четной степени  .
.
Корень нечетной степени из отрицательного числа – отрицательное число; из положительного – положительное.

Корень четной степени берется только из неотрицательного числа. Само значение корня четной степени может быть только неотрицательным.

 .
.
Пример 4
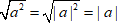
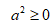 , следовательно, корень из этого выражения существует. При этом значение
, следовательно, корень из этого выражения существует. При этом значение  может быть любым. Если действовать по правилам степеней без модуля, имеем:
может быть любым. Если действовать по правилам степеней без модуля, имеем:
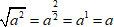 .
.
В случае отрицательного  получаем, что корень четной степени равен отрицательному числу, что невозможно.
получаем, что корень четной степени равен отрицательному числу, что невозможно.
Пример 5
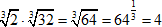
Так как корень – это степень, то можем воспользоваться правилом «степень произведения равна произведению степеней».
Пример 6
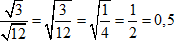
Частное степеней равно степени частного, поэтому занесем всю дробь под общий корень.
Пример 7
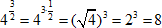
Представим число 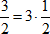 в виде произведения, чтобы можно было воспользоваться правилом «При возведении степени в степень показатели перемножаются, а основание не меняется» в обратную сторону.
в виде произведения, чтобы можно было воспользоваться правилом «При возведении степени в степень показатели перемножаются, а основание не меняется» в обратную сторону.
Помимо выражений с числами, в заданиях часто встречаются выражения с символьными переменными. К счастью, выписанные нами формулы, продолжают работать и в этом случае.
Пример 8

Возведем степень в степень, перемножая показатели. Так как все основания одинаковые, то заменим произведение степеней на сумму показателей, а частное – на разность. Основание при этом не меняем.
Пример 9
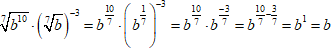
Перепишем корень как дробный показатель. Заменим возведение степени в степень на произведение показателей. Затем преобразуем произведение степеней, сложив их показатели.






















