

4. Планиметрия
 Читать 0 мин.
Читать 0 мин.
4.3. Треугольники
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
СВОЙСТВА ТРЕУГОЛЬНИКА:
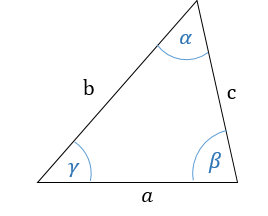
1. Сумма углов в треугольнике равна α + β + γ = 180°.
2. Против большей стороны находится больший угол; против меньшего угла находится меньшая сторона. Отсюда следует, что если:
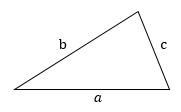
a < b < c, то α < β < γ и наоборот.
3. Сумма длин двух любых сторон треугольника всегда больше длины третьей стороны:
a + b > c.
Если это правило не выполняется — треугольник не существует.
4. Формулы площади треугольника:
|
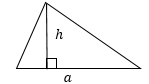
1 (через высоту) |
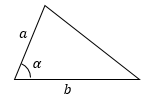
2 (через две стороны и синус угла между ними) |
3 (формула Герона) |
|
|
|
|
|
|
|
|
|
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. |
Площадь треугольника равна половине произведения его сторон на синус угла между ними. |
Площадь треугольника равна квадратному корню из произведения его полупериметра на разности полупериметра и каждой из его сторон. |
5. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
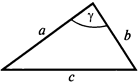
с² = а² + b² – 2ab · cosγ
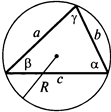
6. Теорема синусов: Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.

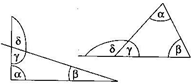
7. Внешний угол треугольника — δ, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α + β = δ).
ВИДЫ ТРЕУГОЛЬНИКОВ:
Треугольники бывают:
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).
Треугольник называется:
- равнобедренным, если две его стороны равны;
- равносторонним, если все три стороны равны;
- разносторонним, если все его стороны разные.
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА:
БИССЕКТРИСА
Биссектриса ― луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части.
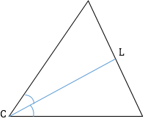
Свойства биссектрисы треугольника:
1. Все три биссектрисы треугольника пересекаются в одной точке. Эта точка — центр вписанной в треугольник окружности.
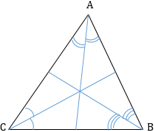
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.
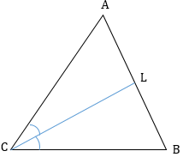

3. Формулы для биссектрисы треугольника. Если а и b — стороны треугольника, γ — угол между ними, l — биссектриса треугольника, проведённая из вершины этого угла, а а' и b' — отрезки, на которые биссектриса делит третью сторону треугольника, то

МЕДИАНА
Медиана ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
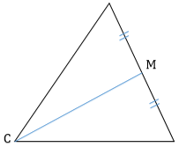
Свойства медианы треугольника:
1. Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и точкой пересечения делятся в отношении 2 к 1, считая от вершины.
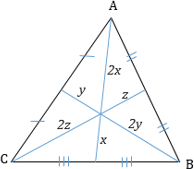
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Формула для медианы треугольника. Если стороны треугольника a и b, mc — медиана треугольника, проведённая к стороне c, то

ВЫСОТА
Высота — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).
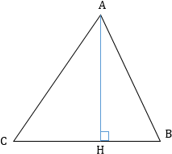
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника (для остроугольного треугольника),
- совпадать с его стороной (являться катетом прямоугольного треугольника),
- проходить вне треугольника (для тупоугольного треугольника).
Свойства высоты треугольника:
1. Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.
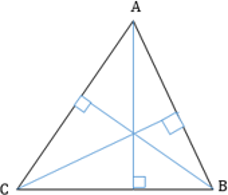
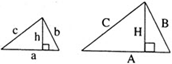
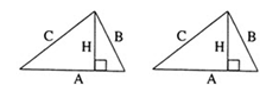
2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
3. Если в треугольнике две высоты равны, то треугольник — равнобедренный.
4. Если CC₁ и АА₁ — высоты треугольника АВС, то треугольник ВА₁С₁ подобен треугольнику АВС, причём коэффициент подобия равен cos B.
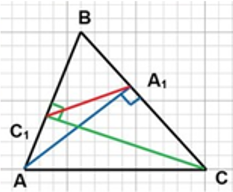
Сложные теоремы:
5. Если Н — точка пересечения высот треугольника AВС, а О — центр его описанной окружности, то отрезок АН вдвое больше расстояния от точки О до середины стороны ВС. То есть AH = 2OM.
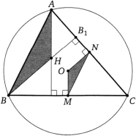
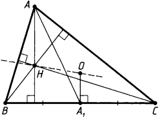
6. Если Н — точка пересечения высот треугольника AВС, М — точка пересечения медиан треугольника AВС, а О — центр его описанной окружности, то точки О, H и М лежат на одной прямой (прямая Эйлера), причём точка М лежит на отрезке ОН и ОМ : МН = 1 : 2.
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Срединный перпендикуляр треугольника — прямая, перпендикулярная стороне треугольника и проходящая через его середину.
Все три срединных перпендикуляра треугольника пересекаются в одной точке, которая является центром описанной около треугольника окружности.
СРЕДНЯЯ ЛИНИЯ
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника
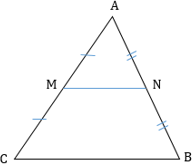
Свойства средней линии треугольника:
- Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
MN||BC,MN = 1/2 BC
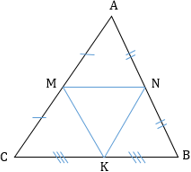
- В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.

ПОДОБИЕ И РАВЕНСТВО ТРЕУГОЛЬНИКОВ
|
Подобные треугольники |
Равные треугольники |
|
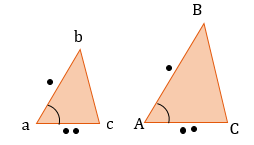
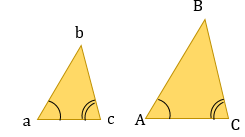
Треугольники подобны, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами и другими линейными величинами (высоты, медианы, биссектрисы и периметры):
Также сохраняется внутреннее отношение длин:
|
Два треугольника равны, если у них соответствующие стороны равны и соответствующие углы равны (треугольники равны, если их можно совместить наложением). |
|
Признаки подобия треугольников: 1. По двум пропорциональным сторонам и углу между ними: 2.
3. По двум равным углам (тогда и третьи тоже будут равны) 4.
5. По трем пропорциональным сторонам:
|
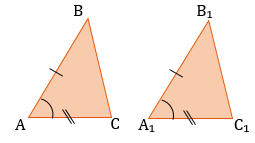
Признаки равенства треугольников: 1. По двум сторонам и углу между ними:
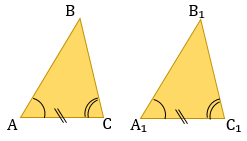
2. По стороне и двум прилежащим к ней углам.
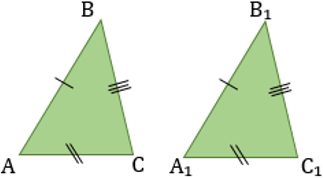
3. По трем сторонам.
|
ОСОБЫЕ ТРЕУГОЛЬНИКИ И ИХ СВОЙСТВА:
«Особенными», то есть обладающими какими — то дополнительными свойствами, считаются:
- равнобедренный,
- равносторонний
- прямоугольный треугольники.
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Равнобедренный треугольник ― это треугольник, у которого две стороны равны (АВ = АС).
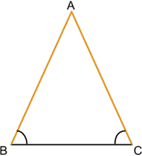
Равные стороны (АВ и АС) в таком треугольнике называются боковыми, а оставшаяся третья сторона (ВС) ― основанием.
Свойства равнобедренного треугольника:
1. Углы при основании равны (∠АВС = ∠АСВ).
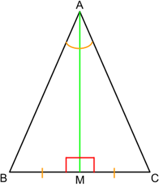
2. Медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (∠ВАМ = ∠МАС).
Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠В = 100° (по сумме смежных углов). Значит, и ∠С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠А = 100°, а ∠В = ∠С = 40°.
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Равносторонний треугольник ― треугольник, у которого все три стороны равны
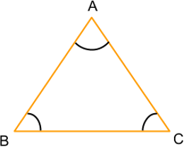
Свойства равностороннего треугольника:
1. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°/3 = 60°).
2. Медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
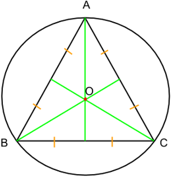
1. Центры вписанной и описанной окружностей совпадают.
2. Формулы 2 и 3 для площади треугольника превращаются в одну формулу:
— Через синус (так как все стороны равны и каждый угол равен 60°):

— Формула Герона (так как все стороны равны):


ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
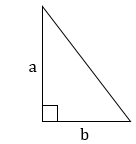
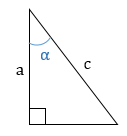
Прямоугольный треугольник ― треугольник, у которого один угол равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (АВ), а две другие стороны ― катетами (АС и ВС).
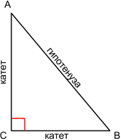
Свойства прямоугольного треугольника:
1. В любом прямоугольном треугольнике гипотенуза всегда больше катета (против большего угла лежит большая сторона, и наоборот).
2. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов
АВ2 = АС2 + ВС2
Теорема, обратная теореме Пифагора: Если для сторон произвольного треугольника выполняется отношение АВ2= АС2 + ВС2, то треугольник является прямоугольным.
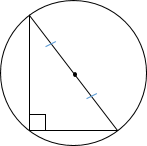
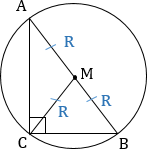
3. Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на середине гипотенузы (доказательство: прямой ∠С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром).
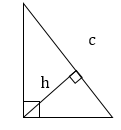
Высота, проведенная к гипотенузе, разбивает треугольник на два подобных прямоугольных треугольника, каждый из которых подобен исходному треугольнику 
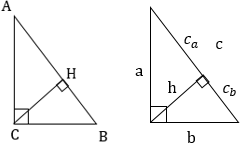
4. Высота, проведенная к гипотенузе, равна:
- Произведению катетов, деленному на гипотенузу

- Среднему геометрическому из произведений отрезков, на которые гипотенуза делится высотой
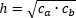
5. Медиана, проведенная к гипотенузе равна половине гипотенузы, то есть радиусу описанной около треугольника окружности.
|
6. Формулы площади прямоугольного треугольника:
|
ЗОЛОТОЙ И СЕРЕБРЯНЫЙ ТРЕУГОЛЬНИКИ:
|
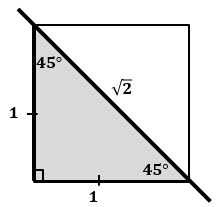
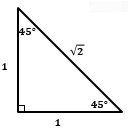
Серебряный треугольник — треугольник с углами 45°, 45° и 90° (разрубленный по диагонали квадрат)
Отношение сторон в серебряном треугольнике:
|
— треугольник с углами 30°, 60° и 90°. Отношение сторон в золотом треугольнике:
|


















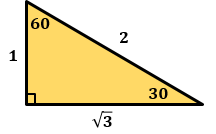 Золотой треугольник
Золотой треугольник




















